Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Бодлого №8060
Бүх ирмэг нь $a$ урттай зөв гурвалжин призм $ABCA_1B_1C_1$-ийн $B,C$ оройнууд ба $A_1C_1$ ирмэгийн дунджийг дайрсан хавтгайгаар призмээс таслагдсан огтлогдсон пирамидын эзлэхүүнийг ол.
A.$\dfrac{9\sqrt3}{64}a^3$ B.$\dfrac{\sqrt3}{8}a^3$ C.$\dfrac16a^3$ D.$\dfrac{12\sqrt3}{77}a^3$ E.$\dfrac{7\sqrt3}{48}a^3$
Бодлогын төрөл:Сонгох
Амжилтын хувь:7.14%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Огтлогдсон пирамидын эзлэхүүн:
$$V=\dfrac13(S_1+\sqrt{S_1S_2}+S_2)h$$
Бодолт:Параллел хавтгайнуудыг огтлолж буй тул $BC\parallel MN$ байна. Нөгөө талаас $A_1M=MC_1$ тул $MN$ нь $A_1B_1C_1$ гурвалжны дундаж шугам болно. Иймд $A_1MN$ нь $\dfrac{a}{2}$ талтай зөв гурвалжин болно. Бидний олох зүйл нь дээд суурь нь $\dfrac{a}{2}$ талтай зөв гурвалжин, доод суурь нь $a$ талтай зөв гурвалжин байдаг $a$ өндөртэй огтлогдсон пирамидын эзлэхүүн юм.
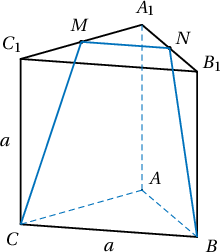Дээд суурийн талбай нь $S_1=\dfrac{\sqrt3\cdot\left(\frac{a}{2}\right)^2}{4}=\dfrac{\sqrt3 a^2}{16}$, доод суурийн талбай нь $S_2=\dfrac{\sqrt3 a^2}{4}$ тул огтлогдсон пирамидын эзлэхүүн нь
\begin{align*}
V&=\dfrac13\left(\dfrac{\sqrt3 a^2}{16}+\sqrt{\dfrac{\sqrt3 a^2}{16}\cdot\dfrac{\sqrt3 a^2}{4}}+\dfrac{\sqrt3 a^2}{4}\right) a\\
&=\dfrac13\left(\dfrac{\sqrt3 a^2}{16}+\dfrac{\sqrt3 a^2}{8}+\dfrac{\sqrt3 a^2}{4}\right) a=\dfrac{7\sqrt3a^3}{48}
\end{align*}