Гармоник цувааг тодорхой интеграл ашиглан үнэлэх
Огноо: 2018-08-17,
Нийтэлсэн: Балхүүгийн Батбаясгалан
Нийтэлсэн: Балхүүгийн Батбаясгалан
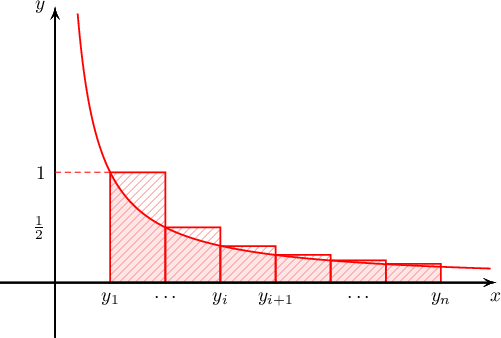
$f(x)=\dfrac{1}{x}$ гээд $\displaystyle\int_1^n f(x)\,\mathrm{d}x$ интеграл ашиглан Гармоник цуваа сарнидаг болохыг үзүүлье. $\displaystyle\int_1^n f(x)\,\mathrm{d}x$ интеграл нь зурагт будагдсан хэсгийн талбайтэй тэнцүү байна.
$[1,n]$ завсарыг $n-1$ ширхэг 1 урттай хэсгүүдэд хуваагаад хуваалтын цэгүүдийг $y_1=1$, $y_2=2,\ldots,y_n=n$ гэвэл $$1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\cdots+\dfrac{1}{n}\ge\int_1^n \dfrac{1}{x} dx=\ln n$$ болох нь зургаас харагдаж байна. $n\to\infty$ үед $\ln n\to\infty$ тул гармоник цуваа сарнина.
Энэ нийтлэлийг 10657 удаа уншсан.
Уншигчдын сэтгэгдэл
Erdene Delgersuren 2019-01-19 19:48
55555