ММО-38, 10-р анги
Бодлогын тоо: 6 Хугацаа: 540 мин
1. $n$ ба $k$ ($n\ge k$) нь өгөгдсөн натурал тоонууд. $A_1,A_2,\ldots,A_n$ нь $A$-ын дэд олонлогууд ба эдгээрийн дурын $k$-ийнх нь нэгдэл $A$ ба $k-1$-ийнх нь $A$-аас ялгаатай бол $\min|A|$-г ол.
Заавар Бодолт
Заавар.
Бодолт. $B_i=\overline{A_i}=A\setminus A_i$, $i\in[n]$ гэе. Аливаа $X_1,\ldots, X_t$ олонлогуудын хувьд
$$\bigcup X_i=A\Leftrightarrow \bigcap \overline{X_i}=\varnothing$$
тул бодлогын нөхцөлөөс $B_i$ олонлогуудын аль ч $k-1$ нь ерөнхий элементтэй, аль ч $k$ нь ерөнхий элементгүй болно.
$X\subseteq[n]$ дэд олонлогийн хувьд $S_{X}=\bigcap\limits_{i\in X} B_i$ гэе. Тэгвэл аливаа $k-1$ элементтэй $X\subseteq[n]$ олонлогийн хувьд $S_X\neq\varnothing$, аливаа $k$ элементтэй $Y\subseteq[n]$ олонлогийн хувьд $S_Y=\varnothing$ байна.
$X_1\neq X_2$ бол $S_{X_1}\cap S_{X_2}=\varnothing$ болохыг харуулъя. Эсрэгээс нь $x\in S_{X_1}\cap S_{X_2}$ гэе. $X_1\neq X_2$, $|X_1|=|X_2|=k-1$ тул $i\not\in X_1$, $i\in X_2$ байх $i\in[n]$ оршин байна. $Y=X_1\cup \{i\}$ гэвэл $|Y|=k$ ба $x\in S_Y\neq\varnothing$ болж зөрчил үүсч байна.
Иймд $$\binom{n}{k-1}\le \sum_{\substack{X\subseteq [n],\\ |X|=k-1}} |S_X|=\big|\bigcup_{\substack{X\subseteq [n],\\ |X|=k-1}} S_X\big|\le |A|$$ байна.
Одоо ямар нэг $\dbinom{n}{k-1}$ элементтэй $A$ олонлогийн хувьд бодлогын нөхцөлийг хангах $A_1,A_2,\ldots,A_n$ дэд олонлогууд олдохыг харуулахад хангалттай. $$A=\{X\colon |X|=n-1, X\subseteq[n]\}$$ ба $$B_i=\{X\colon i\in X\in A\},\quad A_i=A\setminus B_i$$ нь бодлогын нөхцөлийг хангана.
$X\subseteq[n]$ дэд олонлогийн хувьд $S_{X}=\bigcap\limits_{i\in X} B_i$ гэе. Тэгвэл аливаа $k-1$ элементтэй $X\subseteq[n]$ олонлогийн хувьд $S_X\neq\varnothing$, аливаа $k$ элементтэй $Y\subseteq[n]$ олонлогийн хувьд $S_Y=\varnothing$ байна.
$X_1\neq X_2$ бол $S_{X_1}\cap S_{X_2}=\varnothing$ болохыг харуулъя. Эсрэгээс нь $x\in S_{X_1}\cap S_{X_2}$ гэе. $X_1\neq X_2$, $|X_1|=|X_2|=k-1$ тул $i\not\in X_1$, $i\in X_2$ байх $i\in[n]$ оршин байна. $Y=X_1\cup \{i\}$ гэвэл $|Y|=k$ ба $x\in S_Y\neq\varnothing$ болж зөрчил үүсч байна.
Иймд $$\binom{n}{k-1}\le \sum_{\substack{X\subseteq [n],\\ |X|=k-1}} |S_X|=\big|\bigcup_{\substack{X\subseteq [n],\\ |X|=k-1}} S_X\big|\le |A|$$ байна.
Одоо ямар нэг $\dbinom{n}{k-1}$ элементтэй $A$ олонлогийн хувьд бодлогын нөхцөлийг хангах $A_1,A_2,\ldots,A_n$ дэд олонлогууд олдохыг харуулахад хангалттай. $$A=\{X\colon |X|=n-1, X\subseteq[n]\}$$ ба $$B_i=\{X\colon i\in X\in A\},\quad A_i=A\setminus B_i$$ нь бодлогын нөхцөлийг хангана.
2. $p$ өгөгдсөн анхны тоо. Анх координатын хавтгайн $(0,0)$ цэг дээр байсан даам өөрийн байрлаж байгаа цэгээс $p$ зайд орших бүхэл координаттай цэг рүү шилжих үйлдлийг хийх замаар $(2002,38)$ цэгт очиж чаддаг $p$-ийн боломжит бүх утгыг ол.
Заавар Бодолт
Заавар.
Бодолт. $p=2$ үед очиж чадах нь илэрхий. Иймд бид нөхцөл хангах сондгой анхны $p$-үүдийг хайя.
Эйлер-Фермагийн теоремоор $p=x^2+y^2$ байхаар $x$, $y\in\mathbb N$ олдох зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь $p\equiv 1\pmod{4}$ юм. Мөн $$p=x^2+y^2\Rightarrow p^2=(x^2-y^2)^2+(2xy)^2$$ байна.
$p=4k+3$ үед зөвхөн $(x,y)\to(x,y\pm p)$, $(x,y)\to(x\pm,y)$ шилжилтүүд л боломжтой. Иймд $$(0,0)\to\dots\to(2002,38)$$ бол $p\mid 2002$, $p\mid 38$ байна. Энэ зөвхөн $p=2$ үед л боломжтой. Гэтэл $2\neq 4k+3$ юм.
$p=4k+1$ үед $p^2=a^2+b^2$ ба $(a,b)=1$ байх $a$, $b\in\mathbb Z$ оршин байна. Иймд $$(x,y)\to(x+b,y+a)\to(x+b-b,y+a+a)=(x,y+2a)\qquad(1)$$ $$(x,y)\to(x+a,y-b)\to(x+a-a,y-b-b)=(x,y-2b)\qquad(2)$$ шилжилтүүд боломжтой юм. Нөгөө талаас $(a,b)=1$ тул $au-bv=1$ байх $u$, $v\in\mathbb N$ тоонууд оршин байна. Иймд $$(x,y)\overset{u\times (1)}{\longrightarrow}(x,y+2a u)\overset{v\times (2)}{\longrightarrow}(x,y+2au-2bv)=(x,y+2)$$ болно. Төстэйгээр $(x,y)\to(x+2,y)$ гэж шилжүүлэх боломжтой тул $(2002,38)$ цэгт очих боломжтой юм.
Хариу: $p=2$, $p=4k+1$ хэлбэрийн анхны тоо.
Эйлер-Фермагийн теоремоор $p=x^2+y^2$ байхаар $x$, $y\in\mathbb N$ олдох зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь $p\equiv 1\pmod{4}$ юм. Мөн $$p=x^2+y^2\Rightarrow p^2=(x^2-y^2)^2+(2xy)^2$$ байна.
$p=4k+3$ үед зөвхөн $(x,y)\to(x,y\pm p)$, $(x,y)\to(x\pm,y)$ шилжилтүүд л боломжтой. Иймд $$(0,0)\to\dots\to(2002,38)$$ бол $p\mid 2002$, $p\mid 38$ байна. Энэ зөвхөн $p=2$ үед л боломжтой. Гэтэл $2\neq 4k+3$ юм.
$p=4k+1$ үед $p^2=a^2+b^2$ ба $(a,b)=1$ байх $a$, $b\in\mathbb Z$ оршин байна. Иймд $$(x,y)\to(x+b,y+a)\to(x+b-b,y+a+a)=(x,y+2a)\qquad(1)$$ $$(x,y)\to(x+a,y-b)\to(x+a-a,y-b-b)=(x,y-2b)\qquad(2)$$ шилжилтүүд боломжтой юм. Нөгөө талаас $(a,b)=1$ тул $au-bv=1$ байх $u$, $v\in\mathbb N$ тоонууд оршин байна. Иймд $$(x,y)\overset{u\times (1)}{\longrightarrow}(x,y+2a u)\overset{v\times (2)}{\longrightarrow}(x,y+2au-2bv)=(x,y+2)$$ болно. Төстэйгээр $(x,y)\to(x+2,y)$ гэж шилжүүлэх боломжтой тул $(2002,38)$ цэгт очих боломжтой юм.
Хариу: $p=2$, $p=4k+1$ хэлбэрийн анхны тоо.
3. $AB\neq BC$ байх $ABC$ гурвалжинд багтсан тойрог $AB$ ба $BC$ талуудыг харгалзан $M$ ба $N$ цэгээр шүргэв. $MC$ ба $AN$ хэрчмүүд багтсан тойргийг $S$ ба $Q$ цэгээр огтлох бол $MN$, $SQ$, $AC$ шулуунууд нэг цэгт огтлолцохыг батал.
Заавар Бодолт
Заавар.
Бодолт. $SQ\cap AC=L$ гэж тэмдэглэе.
$$\dfrac{CN}{NB}\cdot\dfrac{BM}{MA}\cdot\dfrac{AL}{LC}=1$$
болохыг харуулбал Менелайн теоремоор $M$, $N$, $L$ гурван цэг нэг шулуун дээр орших тул бодлого бодогдоно.
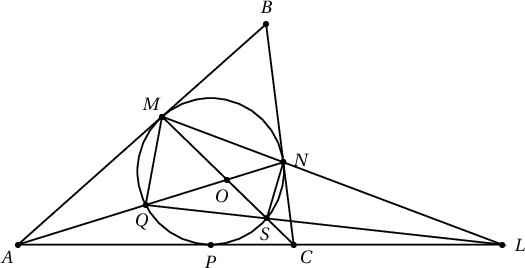Багтсан тойрог $AC$ талыг $P$ цэгт шүргэнэ гэе.
$$\triangle NSC\sim\triangle MNC\Rightarrow\dfrac{MN}{NS}=\dfrac{MC}{NC}$$
$$\triangle AQM\sim\triangle AMN\Rightarrow\dfrac{MN}{MQ}=\dfrac{AN}{AM}$$
болно. Эндээс
$$MN=\dfrac{NS\cdot MC}{NC}=\dfrac{MQ\cdot AN}{AM}$$
буюу
$$\dfrac{AM\cdot NS\cdot MC}{NC\cdot MQ\cdot AN}=1\qquad(*)$$
$MC\cap AN=O$ гэе. Тэгвэл
$$\triangle MOQ\sim\triangle NOS\Rightarrow\dfrac{MQ}{NS}=\dfrac{QO}{OS}$$
болно. Шүргэгч огтлогчийн чанараас
$$\dfrac{AN}{AM}=\dfrac{AP}{AQ},\quad \dfrac{MC}{CN}=\dfrac{CP}{CS}$$
байхыг $(*)$-д орлуулъя. Тэгвэл
$$\dfrac{AQ}{AP}\cdot\dfrac{PC}{CS}\cdot\dfrac{SO}{OQ}=1\qquad(1)$$
болно. Хэрэв $QS\parallel AC$ байвал $MN\parallel AC$ болох буюу энэ нь $AB\neq BC$ гэдэгт зөрчинө.
Менелайн теоремоор $$\dfrac{CS}{SO}\cdot\dfrac{OQ}{QA}\cdot\dfrac{AL}{LC}=1\qquad(2)$$ $(1)$, $(2)$ болон $CP=CN$, $AP=AM$-аас $$\dfrac{AL}{LC}\cdot\dfrac{CP}{AP}=1\Rightarrow \dfrac{AL}{LC}\cdot\dfrac{CN}{AM}=1$$ болох нь гарна. $BN=BM$ учир $$\dfrac{CN}{NB}\cdot\dfrac{BM}{MA}\cdot\dfrac{AL}{LC}=1$$ болж батлах зүйл батлагдав.
Менелайн теоремоор $$\dfrac{CS}{SO}\cdot\dfrac{OQ}{QA}\cdot\dfrac{AL}{LC}=1\qquad(2)$$ $(1)$, $(2)$ болон $CP=CN$, $AP=AM$-аас $$\dfrac{AL}{LC}\cdot\dfrac{CP}{AP}=1\Rightarrow \dfrac{AL}{LC}\cdot\dfrac{CN}{AM}=1$$ болох нь гарна. $BN=BM$ учир $$\dfrac{CN}{NB}\cdot\dfrac{BM}{MA}\cdot\dfrac{AL}{LC}=1$$ болж батлах зүйл батлагдав.
4. Үржвэр нь яг $13$ ялгаатай анхны тоон хуваагчтай байх ялгаатай $131$ натурал тоо өгөгджээ. Тэдгээрээс үржвэр нь бүтэн квадрат байх $4$ тоог сонгон авч болно гэж батал.
Заавар Бодолт
Заавар.
Бодолт. Зэргүүдийн тэгш сондгой нь чухал тул
$$a=p_1^{\alpha_1}\cdot p_2^{\alpha_2}\cdot\dots\cdot p_{13}^{\alpha_{13}}\to\alpha=(\alpha_1,\alpha_2,\ldots,a_{13})\pmod{2}$$
буулгалтаар үүсэх векторуудыг авч үзье. Эдгээр векторуудын дунд нийлбэр нь $(0,0,\dots,0)\pmod{2}$ байх 4 вектор олдвол тэдгээрт харгалзах тоонуудын үржвэр нь бүтэн квадрат байх нь ойлгомжтой.
$\alpha+\beta$ хэлбэрийн нийлбэрүүдийг авч үзье. Нийт $C_{131}^2=8515$ нийлбэр зохиож болно. Нөгөө талаас ялгаатай векторын тоо $2^{13}=8192$ тул Дирихлейн зарчмаар тэнцүү хоёр нийлбэр олдоно. Эдгээр нь $\alpha+\beta$, $\gamma+\delta$ гэе. Хэрвээ $\alpha$, $\beta$, $\gamma$, $\delta$ векторууд ялгаатай бол $$\alpha+\beta+\gamma+\delta\equiv(0,0,\dots,0)\pmod{2}$$ тул бидний хайж байгаа тоонууд олдлоо. Хэрвээ $\alpha=\gamma$ бол үлдэх векторуудаас яг ижил аргаар ($C_{129}^2>2^{13}$ тул боломжтой) нийлбэр нь $(0,0,\dots,0)\pmod{2}$ байх ялгаатай 4 дөрвөн вектор, эсвэл $\mu=\nu$ хоёр вектор олж болно. Эхний тохиолдол нь өмнөх тохиолдолтой ижил ба хоёр дахь тохиолдолд $$\alpha+\gamma+\mu+\nu\equiv(0,0,\dots,0)\pmod{2}$$ тул бодлого бодогдов.
$\alpha+\beta$ хэлбэрийн нийлбэрүүдийг авч үзье. Нийт $C_{131}^2=8515$ нийлбэр зохиож болно. Нөгөө талаас ялгаатай векторын тоо $2^{13}=8192$ тул Дирихлейн зарчмаар тэнцүү хоёр нийлбэр олдоно. Эдгээр нь $\alpha+\beta$, $\gamma+\delta$ гэе. Хэрвээ $\alpha$, $\beta$, $\gamma$, $\delta$ векторууд ялгаатай бол $$\alpha+\beta+\gamma+\delta\equiv(0,0,\dots,0)\pmod{2}$$ тул бидний хайж байгаа тоонууд олдлоо. Хэрвээ $\alpha=\gamma$ бол үлдэх векторуудаас яг ижил аргаар ($C_{129}^2>2^{13}$ тул боломжтой) нийлбэр нь $(0,0,\dots,0)\pmod{2}$ байх ялгаатай 4 дөрвөн вектор, эсвэл $\mu=\nu$ хоёр вектор олж болно. Эхний тохиолдол нь өмнөх тохиолдолтой ижил ба хоёр дахь тохиолдолд $$\alpha+\gamma+\mu+\nu\equiv(0,0,\dots,0)\pmod{2}$$ тул бодлого бодогдов.
5. $a_0,a_1,a_2,\ldots$ гэсэн эерэг тоонуудын төгсгөлгүй дараалал өгөгдөв. $1+a_n\ge\sqrt[n]{2}a_{n-1}$ байх $n$ дугаар төгсгөлгүй олон олдохыг батал.
Заавар Бодолт
Заавар.
Бодолт. Эсрэгээс нь $n$-ийн утгыг төгсгөлөг гэж үзвэл $\exists N\forall (n>N):$
$$1+a_n < a_{n-1}\cdot 2^{\frac1n}\qquad(*)$$
үнэн байна. Хялбарчлах үүднээс $N=0$ гэж үзэж болно.
$(*)$-оос \begin{align*} 1+a_n&< a_{n-1}\cdot 2^{\frac{1}{n}}\\ 2^{\frac{1}{n}}+a_{n-1}\cdot 2^{\frac{1}{n}}&< a_{n-2}\cdot 2^{\frac{1}{n}+\frac{1}{n-1}}\\ 2^{\frac{1}{n}+\frac{1}{n-1}}+a_{n-2}\cdot 2^{\frac{1}{n}+\frac{1}{n-1}}&< a_{n-3}\cdot 2^{\frac{1}{n}+\frac{1}{n-1}+\frac{1}{n-2}}\\ \dots\dots&\dots\dots \end{align*} гэж гарах ба эдгээрийг нэмбэл $$1+\sum_{i=0}^{n-3}2^{\frac{1}{n}+\frac{1}{n-1}+\dots+\frac{1}{n-i}}+a_n < a_1\cdot 2^{\frac{1}{n}+\frac{1}{n-1}+\dots+\frac{1}{2}}$$ ба $a_n>0$ тул $$\sum_{i=0}^{n-3}2^{\frac{1}{n}+\frac{1}{n-1}+\dots+\frac{1}{n-i}} < a_1\cdot 2^{\frac{1}{n}+\frac{1}{n-1}+\dots+\frac{1}{2}}$$ буюу $$\sum_{i=0}^{n-3} 2^{-\left(\frac{1}{2}+\frac{1}{3}+\dots+\frac{1}{n-i-1}\right)} < a_1\qquad(*)$$ болно. Одоо зүүн гар талын илэрхийлэл $n\to+\infty$ үед $+\infty$ рүү тэмүүлнэ гэж харуулбал $+\infty = a_1$ болж зөрчил үүсэх тул батлах зүйл маань батлагдана. $$S_n=\dfrac{1}{2}+\dfrac{1}{3}+\dots+\dfrac{1}{n}$$ гэвэл $$(*)\Leftrightarrow \sum_{i=0}^{n-3}2^{-S_{n-i-1}} < a_1\Leftrightarrow \sum_{k=4}^{n+1} 2^{-S_k} < a_1$$ болно. Аливаа $n\in\mathbb N$-ийн хувьд $$\ln n+C_1 < S_n < \ln n+C_2$$ байх $C_1$, $C_2$ тоо олдоно гэдгийг ашиглая: $$2^{-C_2}\cdot\sum_{i=2}^{n-1}2^{-\ln i}=\sum_{i=0}^{n-3}2^{-\ln (n-i-1)-C_2} < \sum_{i=0}^{n-3} 2^{-S_{n-i-1}}$$ тул $$2^{-\ln 2}+2^{-\ln 3}+2^{-\ln 4}+\cdots $$ цуваа сарнина гэдгийг харуулахад хангалттай. Үнэндээ $$\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dots=e^{-\ln 2}+e^{-\ln 3}+e^{-\ln 4}+\cdots < 2^{-\ln 2}+2^{-\ln 3}+2^{-\ln 4}+\cdots $$ тул дээрх цуваа сарнина.
$(*)$-оос \begin{align*} 1+a_n&< a_{n-1}\cdot 2^{\frac{1}{n}}\\ 2^{\frac{1}{n}}+a_{n-1}\cdot 2^{\frac{1}{n}}&< a_{n-2}\cdot 2^{\frac{1}{n}+\frac{1}{n-1}}\\ 2^{\frac{1}{n}+\frac{1}{n-1}}+a_{n-2}\cdot 2^{\frac{1}{n}+\frac{1}{n-1}}&< a_{n-3}\cdot 2^{\frac{1}{n}+\frac{1}{n-1}+\frac{1}{n-2}}\\ \dots\dots&\dots\dots \end{align*} гэж гарах ба эдгээрийг нэмбэл $$1+\sum_{i=0}^{n-3}2^{\frac{1}{n}+\frac{1}{n-1}+\dots+\frac{1}{n-i}}+a_n < a_1\cdot 2^{\frac{1}{n}+\frac{1}{n-1}+\dots+\frac{1}{2}}$$ ба $a_n>0$ тул $$\sum_{i=0}^{n-3}2^{\frac{1}{n}+\frac{1}{n-1}+\dots+\frac{1}{n-i}} < a_1\cdot 2^{\frac{1}{n}+\frac{1}{n-1}+\dots+\frac{1}{2}}$$ буюу $$\sum_{i=0}^{n-3} 2^{-\left(\frac{1}{2}+\frac{1}{3}+\dots+\frac{1}{n-i-1}\right)} < a_1\qquad(*)$$ болно. Одоо зүүн гар талын илэрхийлэл $n\to+\infty$ үед $+\infty$ рүү тэмүүлнэ гэж харуулбал $+\infty = a_1$ болж зөрчил үүсэх тул батлах зүйл маань батлагдана. $$S_n=\dfrac{1}{2}+\dfrac{1}{3}+\dots+\dfrac{1}{n}$$ гэвэл $$(*)\Leftrightarrow \sum_{i=0}^{n-3}2^{-S_{n-i-1}} < a_1\Leftrightarrow \sum_{k=4}^{n+1} 2^{-S_k} < a_1$$ болно. Аливаа $n\in\mathbb N$-ийн хувьд $$\ln n+C_1 < S_n < \ln n+C_2$$ байх $C_1$, $C_2$ тоо олдоно гэдгийг ашиглая: $$2^{-C_2}\cdot\sum_{i=2}^{n-1}2^{-\ln i}=\sum_{i=0}^{n-3}2^{-\ln (n-i-1)-C_2} < \sum_{i=0}^{n-3} 2^{-S_{n-i-1}}$$ тул $$2^{-\ln 2}+2^{-\ln 3}+2^{-\ln 4}+\cdots $$ цуваа сарнина гэдгийг харуулахад хангалттай. Үнэндээ $$\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dots=e^{-\ln 2}+e^{-\ln 3}+e^{-\ln 4}+\cdots < 2^{-\ln 2}+2^{-\ln 3}+2^{-\ln 4}+\cdots $$ тул дээрх цуваа сарнина.
6. $ABC$ гурвалжны $BC$, $CA$, $AB$ талын дунджууд нь харгалзан $A_1$, $B_1$, $C_1$. $C_1A_1$ хэрчим дээр $\dfrac{C_1K}{KA_1}=\dfrac{BC+AC}{AC+AB}$ байх $K$ цэгийг, $A_1B_1$ хэрчим дээр $\dfrac{A_1L}{LB_1}=\dfrac{AC+AB}{BC+AB}$ байх $L$ цэгийг тус тус авав. $BK\cap CL=S$ бол $\measuredangle C_1A_1S=\measuredangle B_1A_1S$ болохыг батал.
Заавар Бодолт
Заавар.
Бодолт.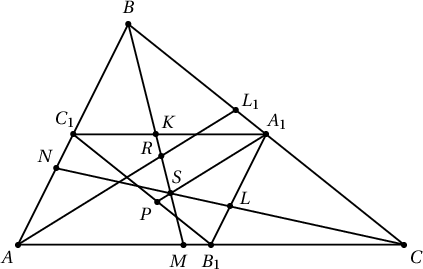 
$\measuredangle C_1A_1B$-ийн биссектрис $A_1P$ нь $S$-ийг дайрна гэж харуулъя. Менелайн теоремоор
$$\dfrac{AN}{NB}\cdot\dfrac{BS}{SM}\cdot\dfrac{MC}{CA}=1$$
ба
$$\dfrac{NB}{AN}=\dfrac{LA_1}{BL}=\dfrac{b+c}{a+c},$$
$$\dfrac{CA}{MC}=1+\dfrac{AM}{MC}=1+\dfrac{C_1K}{KA_1}=\dfrac{a+c+2b}{b+c}$$
тул
$$\dfrac{BS}{SM}=\dfrac{b+c}{a+c}\cdot\dfrac{a+c+2b}{b+c}=\dfrac{a+c+2b}{a+c}$$
байна. Одоо $BM\cap A_1P=Q$ гээд
$$\dfrac{BQ}{QM}=\dfrac{a+c+2b}{a+c}$$
гэж харуулахад $S\equiv Q$ болж батлагдана. $AL_1\parallel A_1P$ тул
$$\dfrac{BR}{BQ}=\dfrac{BL_1}{BA_1}=\dfrac{\frac{ac}{b+c}}{\frac{a}{2}}=\dfrac{2c}{b+c}\Rightarrow BR=\dfrac{2c}{b+c}\cdot BQ$$
байна.
$$AM=\dfrac{AM}{AC}\cdot b=\dfrac{C_1K}{C_1A_1}\cdot b=\dfrac{b(a+c)}{a+c+2b}$$
тул биссектрисийн чанараар
$$\dfrac{RM}{BR}=\dfrac{AM}{AB}=\dfrac{b(a+b)}{c(a+c+2b)}$$
болно. Иймд
$$\dfrac{BM}{BR}=\dfrac{RM}{BR}+1=\dfrac{b(a+b)+c(a+c+2b)}{c(a+c+2b)}\Rightarrow$$
\begin{align*}
BM&=\dfrac{b(a+b)+c(a+c+2b)}{c(a+c+2b)}\cdot BR\\
&=\dfrac{b(a+b)+c(a+c+2b)}{c(a+c+2b)}\cdot\dfrac{2c}{b+c}\cdot BQ
\end{align*}
тул
\begin{align*}
\dfrac{BM}{BQ}&=\dfrac{2(ab+b^2+ac+c^2+2bc)}{(a+c+2b)(b+c)}\\
&=\dfrac{2(b+c)(a+b+c)}{(a+c+2b)(b+c)}\\
&=\dfrac{2(a+b+c)}{a+c+2b}=1+\dfrac{QM}{BQ}
\end{align*}
болно. Эндээс
$$\dfrac{QM}{BQ}=\dfrac{2(a+b+c)}{a+c+2b}-1=\dfrac{a+c}{a+c+2b}$$
буюу
$$\dfrac{BQ}{QM}=\dfrac{a+c+2b}{a+c}$$
болж батлах зүйл батлагдав.