ММО-07, 10-р анги
Бодлогын тоо: 8 Хугацаа: 540 мин
1. $z=|\sin y|$ бол $\log_z(|x|-1)<0$ тэнцэтгэл бишийг хангах $(x,y)$ хосуудын олонлогийг ол.
Заавар Бодолт
Заавар.
Бодолт. Тодорхойлогдох мужаа олбол
$$\left\{\begin{array}{c}
0 < |\sin y| < 1\\
|x| - 1> 0
\end{array}\right.$$
болно. Үүнийг бодвол
$$\left\{\begin{array}{c}
|x| > 1\\
y\neq\dfrac{k\pi}{2}, k\in\mathbb Z
\end{array}\right.$$
гэж гарна.
$\log_{|\sin y|}(|x|-1)<0=\log_{|\sin y|}1$ гэж бичвэл $0<|\sin y|<1$ учир $|x|-1>1$ буюу $|x|>2$ болно. Иймд манай тэнцэтгэл бишийн шийд нь
$$\{(x,y)\mid |x|>2, y\neq\dfrac{k\pi}{2},k\in\mathbb Z\}$$
олонлог болно.
2. Ямар дөрвөн өнцөгтүүдийг шулуунаар огтлоход 2 төсөөтэй 4 өнцөгт үүсэх вэ?
Заавар Бодолт
Заавар.
Бодолт. $AMND$ дөрвөн өнцөгт $BCNM$-тэй төстэй байг.
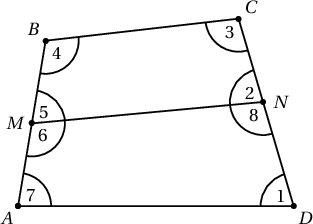 1) $\angle 1=\angle 2$ бол $MN\parallel AD$ учраас уг 2 дөрвөн өнцөгт хоёул трапец болно. Одоо ямар ч трапецийг суурьтай нь параллел шулуунаар ингэж хувааж болно гэж үзүүлье.
1) $\angle 1=\angle 2$ бол $MN\parallel AD$ учраас уг 2 дөрвөн өнцөгт хоёул трапец болно. Одоо ямар ч трапецийг суурьтай нь параллел шулуунаар ингэж хувааж болно гэж үзүүлье.
$BC=a$, $MN=x$, $AD=c$ байг. $$\dfrac{BC}{MN}=\dfrac{a}{x}=\dfrac{x}{c}=\dfrac{MN}{AD}$$ гэдгээс $x=\sqrt{ac}$ болно. $BB_1\parallel CD\parallel MM_1$-ийг татъя. $BB_1$ ба $MN$-ийн огтлолыг $E$ гэе. $\triangle BEM\sim\triangle MM_1A$ учир $$\dfrac{BM}{MA}=\dfrac{ME}{AM_1}=\dfrac{\sqrt{ac}-a}{c-\sqrt{ac}}=\dfrac{\sqrt{a}}{\sqrt{c}}$$ мөн $\dfrac{BC}{MN}=\dfrac{a}{\sqrt{ac}}=\dfrac{\sqrt{a}}{\sqrt{c}}$ тул батлах зүйл батлагдав.
2) $\angle 1=\angle 5$ бол $\angle 3=\angle 6$ болох учир $$\angle1+\angle 3=\angle 5+\angle 6=180^\circ$$ болж мөн $AD\parallel BC$ гэж гарах тул $ABCD$ трапец болно.
3) $\angle 1=\angle 3$ бол $\angle 5=\angle 6=90^\circ$ болно. Энэ үед $\angle 2=\angle 8$ бол $\angle 5+\angle 2=180^\circ$, $AB\parallel CD$ болж $ABCD$ нь мөн л трапец байна. Харин $\angle 2=\angle 7$ бол $\angle 4=\angle 8$, $$180^\circ=\angle 2+\angle 8=\angle 7+\angle 8,\quad \angle 1=90^\circ=\angle 3$$ болох тул $BC\parallel AD$ буюу $ABCD$ мөн л трапец байна.
4) $\angle 1=\angle 4$ бол $\angle 2=\angle 6$ болох тул $AB\parallel CD$ байна. Иймд $ABCD$ нь мөн л трапец болов.

$BC=a$, $MN=x$, $AD=c$ байг. $$\dfrac{BC}{MN}=\dfrac{a}{x}=\dfrac{x}{c}=\dfrac{MN}{AD}$$ гэдгээс $x=\sqrt{ac}$ болно. $BB_1\parallel CD\parallel MM_1$-ийг татъя. $BB_1$ ба $MN$-ийн огтлолыг $E$ гэе. $\triangle BEM\sim\triangle MM_1A$ учир $$\dfrac{BM}{MA}=\dfrac{ME}{AM_1}=\dfrac{\sqrt{ac}-a}{c-\sqrt{ac}}=\dfrac{\sqrt{a}}{\sqrt{c}}$$ мөн $\dfrac{BC}{MN}=\dfrac{a}{\sqrt{ac}}=\dfrac{\sqrt{a}}{\sqrt{c}}$ тул батлах зүйл батлагдав.
2) $\angle 1=\angle 5$ бол $\angle 3=\angle 6$ болох учир $$\angle1+\angle 3=\angle 5+\angle 6=180^\circ$$ болж мөн $AD\parallel BC$ гэж гарах тул $ABCD$ трапец болно.
3) $\angle 1=\angle 3$ бол $\angle 5=\angle 6=90^\circ$ болно. Энэ үед $\angle 2=\angle 8$ бол $\angle 5+\angle 2=180^\circ$, $AB\parallel CD$ болж $ABCD$ нь мөн л трапец байна. Харин $\angle 2=\angle 7$ бол $\angle 4=\angle 8$, $$180^\circ=\angle 2+\angle 8=\angle 7+\angle 8,\quad \angle 1=90^\circ=\angle 3$$ болох тул $BC\parallel AD$ буюу $ABCD$ мөн л трапец байна.
4) $\angle 1=\angle 4$ бол $\angle 2=\angle 6$ болох тул $AB\parallel CD$ байна. Иймд $ABCD$ нь мөн л трапец болов.
3. $ABC$ гурвалжны өнцгүүд нь $3\tg A\cdot\tg B=-1$ гэсэн хамааралтай бол $m_c=R$ болохыг батал. Энд $m_c$ нь $C$ оройгоос гарсан медиан, $R$ нь $ABC$ гурвалжинг багтаасан тойргийн радиус.
Заавар Бодолт
Заавар.
Бодолт. $\angle A$, $\angle B$-ийн аль нэг нь мохоо. Иймд $\angle B>90^\circ$ гэж үзье. $C$ цэгээс $AB$-д перпендикуляр буулгавал $AB$ хэрчмийн үргэлжлэл дээр бууна. Түүний суурь $D$ болог. Тэгвэл
$$\tg\angle A=\dfrac{CD}{AD},\quad\tg\angle B=-\dfrac{CD}{BD},\quad\tg\angle A\cdot\tg\angle B=-\dfrac13\Rightarrow 3CD^2=AD\cdot BD\quad(1)$$
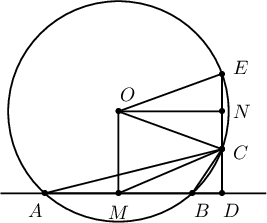 Багтаасан тойрог ба $CD$-ийн огтлолцсон цэг нь $E$ болог. Тэгвэл шүргэгч огтлогчийн теорем ёсоор
$$AD\cdot BD=DE\cdot DC$$
болох тул (1)-ээс
$$3CD^2=CD\cdot DE\Rightarrow 2CD=CE$$
болно.
Багтаасан тойрог ба $CD$-ийн огтлолцсон цэг нь $E$ болог. Тэгвэл шүргэгч огтлогчийн теорем ёсоор
$$AD\cdot BD=DE\cdot DC$$
болох тул (1)-ээс
$$3CD^2=CD\cdot DE\Rightarrow 2CD=CE$$
болно.
Багтаасан тойргийн төвөөс $AB$, $CD$-д перпендикуляр буулгаж суурийг нь $M$, $N$ гэе. Тэгвэл $OM\parallel ED$, $MD\parallel ON$ гэдгээс $OM=ND$, $NC=NE=CD$ болох тул $C$ нь $ND$ хэрчмийн дундаж цэг болно. Иймд $\angle MDC=90^\circ$, $\angle ONC=90^\circ$, $MD=ON$, $NC=CD$ болох тул $$R=OC=CM=m_c$$ болно. Бодлого бодогдов.

Багтаасан тойргийн төвөөс $AB$, $CD$-д перпендикуляр буулгаж суурийг нь $M$, $N$ гэе. Тэгвэл $OM\parallel ED$, $MD\parallel ON$ гэдгээс $OM=ND$, $NC=NE=CD$ болох тул $C$ нь $ND$ хэрчмийн дундаж цэг болно. Иймд $\angle MDC=90^\circ$, $\angle ONC=90^\circ$, $MD=ON$, $NC=CD$ болох тул $$R=OC=CM=m_c$$ болно. Бодлого бодогдов.
4. Бөмбөрцгийн төвийг дайрсан боловч аль ч гурав нь нэг диаметрийг дайраагүй хавтгайнуудаар бөмбөрцгийн гадаргуу хэчнээн хэсэгт хуваагдах вэ?
Заавар Бодолт
Заавар.
Бодолт. $m$ хавтгай авч үзэхэд бөмбөрцгийн гадаргуу нь $F(m)$ хэсэгт хуваагддаг байг. $m$-р хавтгай ба бөмбөрцөг гадаргуугийн огтлолд үүсэх тойрог нь бусад хавтгай бүртэй 2 цэгээр огтлолцож, эдгээр цэгүүдээр $2(m-1)$ хэсэгт хуваагдана. Иймд
$$F(m)=2(m-1)+F(m-1)$$
гэсэн рекуррент харьцаа биелэнэ. $F(1)=2$ гэдгийг анхаарвал
$$F(m)=2+m(m-1)$$
5. $5,13,25,41,61,\dots$ дарааллын эхний $n$ гишүүний нийлбэрийг ол.
Заавар Бодолт
Заавар.
Бодолт. $a_1=5$, $a_{n}=a_{n-1}+4n$, $n\ge 2$ дараалал юм. Иймд
\begin{align*}
a_{n}&=a_1+\sum_{k=1}^{n-1}(4k)+4\cdot (n-1)=5+4\sum_{k=1}^{n-1}k+4n-4\\
&=1+4n+4\cdot\dfrac{(n-1)n}{2}=2n^2+2n+1
\end{align*}
болно. Иймд
\begin{align*}
a_{n}&=\sum_{k=1}^{n}(2k^2+2k+1)\\
&=2\sum_{k=1}^{n}k^2+2\sum_{k=1}^{n}k+n\\
&=2\cdot\dfrac{n(n+1)(2n+1)}{6}+2\cdot\dfrac{n(n+1)}{2}+n\\
&=\dfrac{n\{(n+1)(2n+1)+3(n+1)+3\}}{3}\\
&=\dfrac{n(2n^2+6n+7)}{3}
\end{align*}
6. Дараах тэгшитгэлийг бод.
$$(\sin x)^{\log_{a^{1\cdot 2}}x^x+\log_{a^{2\cdot 3}}x^x+\dots+\log_{a^{n\cdot (n+1)}}x^x}=\left[\cos\left(\dfrac{\pi}{2}-x\right)\right]^x$$
Заавар Бодолт
Заавар.
Бодолт. $$(\sin x)^{x(\log_{a^{1\cdot 2}}x+\log_{a^{2\cdot 3}}x+\dots+\log_{a^{n\cdot (n+1)}}x)}=(\sin x)^x$$
Иймд эсвэл $\sin x=0$, эсвэл $\sin x=1$, эсвэл $0\neq\sin x\neq 1$ ба
$$\log_{a^{1\cdot 2}}x+\log_{a^{2\cdot 3}}x+\dots+\log_{a^{n\cdot (n+1)}}x=1$$
болно.
\begin{align*}
1&=\log_{a^{1\cdot 2}}x+\log_{a^{2\cdot 3}}x+\dots+\log_{a^{n\cdot (n+1)}}x\\
&=\left(\dfrac{1}{1\cdot 2}+\dfrac{1}{2\cdot 3}+\dfrac{1}{3\cdot 4}+\dots+\dfrac{1}{n\cdot(n+1)}\right)\cdot\log_ax\\
&=\left(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dots+\dfrac{1}{n}-\dfrac{1}{n+1}\right)\cdot\log_ax\\
&=\left(1-\dfrac{1}{n+1}\right)\cdot\log_ax=\dfrac{n}{n+1}\cdot\log_ax
\end{align*}
Эндээс $x=a^{\frac{n+1}{n}}$ болов. Тэгшитгэлийн шийдийн олонлог нь
$$\left\{k\pi,\,\dfrac{\pi}{2}+2\pi k,\, a^{\frac{n+1}{n}},\, k\in\mathbb Z\right\}$$
7. $x_1+x_2+x_3+x_4+x_5=104$ тэгшитгэл хэчнээн натурал тоон шийдтэй вэ?
Заавар Бодолт
Заавар. Давталттай хэсэглэлийн томьёо ашиглаж бод.
Бодолт. $$C_{(5)}^{104}=C_{5+104-1}^{104}=\dfrac{108!}{(108-104)!\cdot 104!}=\dfrac{105\cdot 106\cdot 107\cdot 108}{4!}=5359095$$
8. Гурвалжинг багтаасан тойргийн радиус $R$ ба түүнд багтсан тойргийн радиус $r$ бол $R \geq 2r$ болохыг батал.
Заавар Бодолт
Заавар.
Бодолт. Гурвалжны хүндийн төв дээр төвтэй $k=-\dfrac{1}{2}$ коэффициенттэй гомотет авч үзье. $ABC$ гурвалжны дүр $A_1B_1C_1$ нь талуудын дундаж цэгүүдэд оройтой гурвалжин бөгөөд багтаасан тойргийн радиус нь $\dfrac{R}{2}$ байна. $ABC$ гурвалжинд багтсан тойргийн радиус нь $ABC$ гурвалжны 3 тал дээр оройтой аливаа $A_1B_1C_1$ гурвалжныг багтаасан $\omega_1$ тойргийн радиусаас хэтрэхгүй.
Учир нь $\omega_1$ нь $ABC$ гурвалжны талуудтай тус бүр 2 ерөнхий цэгтэй бол $\omega_1$ тойргийн төв дээр төвтэй гомотетоор тойргийг багасгаж аль нэг талыг нь шүргүүлнэ. Дараагийн удаад уг шүргэлтийн цэг дээр төвтэй гомотетоор тойргоо багасгаж дахин өөр нэг талыг нь шүргүүлнэ. Үүний дараа уг шүргэсэн 2 талын ерөнхий орой дээр төвтэй гомотетоор тойргоо багасгаж $ABC$ гурвалжинд багтсан тойрогт шилжүүлж болно.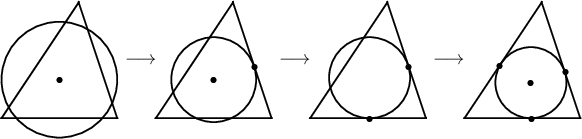 Иймд
$$r\le \dfrac{R}{2}\Rightarrow 2r\le R$$
болж батлагдав. Тэнцэлдээ хүрэх нөхцөл нь $ABC$ гурвалжны медианууд биссектристэйгээ давхцах тул $ABC$ зөв гурвалжин байна.
Иймд
$$r\le \dfrac{R}{2}\Rightarrow 2r\le R$$
болж батлагдав. Тэнцэлдээ хүрэх нөхцөл нь $ABC$ гурвалжны медианууд биссектристэйгээ давхцах тул $ABC$ зөв гурвалжин байна.
Учир нь $\omega_1$ нь $ABC$ гурвалжны талуудтай тус бүр 2 ерөнхий цэгтэй бол $\omega_1$ тойргийн төв дээр төвтэй гомотетоор тойргийг багасгаж аль нэг талыг нь шүргүүлнэ. Дараагийн удаад уг шүргэлтийн цэг дээр төвтэй гомотетоор тойргоо багасгаж дахин өөр нэг талыг нь шүргүүлнэ. Үүний дараа уг шүргэсэн 2 талын ерөнхий орой дээр төвтэй гомотетоор тойргоо багасгаж $ABC$ гурвалжинд багтсан тойрогт шилжүүлж болно.