ММО-23, 10-р анги
Бодлогын тоо: 6 Хугацаа: 540 мин
1. $n\ge 2$ үед $f(n-1)\cdot f(n+1)=f^2(n)-1$ ба $f(1987)=1987$ байх бүх $f\colon\mathbb N\to\mathbb N$ функцийг ол.
Заавар Бодолт
Заавар.
Бодолт. $f(n)=n$ адилтгал функц бодлогын нөхцөлийг хангах нь илэрхий. Одоо бодлогын нөхцөлийг хангах дурын $f(n)$ функц заавал адилтгал функц байна гэж баталъя. $f(n)$ нь өсөх функц болохыг тогтооё. Эсрэгээс нь $f(m)>f(m+1)$ дугаар олдоно гэвэл
$$f(m)\cdot f(m+2)=f^2(m+1)-1 < f^2(m+1) < f(m)\cdot f(m+1)$$
Эндээс $f(m+1)>f(m+2)$. Энэ процессийг индукцээр давтвал дурын $k$-ийн хувьд
$$f(m)>f(m+1)>\dots>f(m+k)$$
Гэтэл $f$ нь натурал утга авдаг тул ийм байж болохгүй.
$$1987=f(1987)>f(1986)>\dots>f(2)>f(1)$$
Эндээс $f(n)=n$ тэнцэтгэл $n\le 1987$ байх бүх $n$ дугаарын хувьд батлагдав. $f(k)=k$ болох нь $k\le n$ байх бүх $k$ дугаарын хувьд шалгагдсан байг гэж үзье.
$$f(n-1)\cdot f(n+1)=f^2(n)-1$$
тэнцэтгэлээс индукцийн таамаглал ёсоор
$$(n-1)f(n+1)=n^2-1\Rightarrow f(n+1)=n+1$$
Ийнхүү $f(n)=n$ тэнцэтгэлийг дурын $n$ дугаарын хувьд биелэгдэхийг индукцээр батлав.
2. $4$ радиустай тойргийг багтаах $ABC$ гурвалжны $C$ оройгоос нөгөө хоёр оройн гадаад өнцгийн биссектрист буулгасан перпендикулярын сууриудын хоорондох зай $21$ ба
$$7\cdot\tg\dfrac{A}2\cdot\tg\dfrac{B}2=2$$
бол талуудыг ол.
Заавар Бодолт
Заавар.
Бодолт. 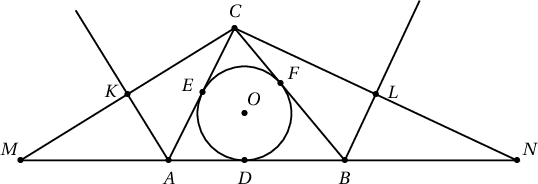 $r=4$, $AB=c$, $AC=b$, $BC=a$, $a+b+c=2p$ гэж тэмдэглэе. $CBN$ ба $CAM$ гурвалжнууд адил хажуутай тул $MN=2p$ байх бөгөөд $KL$ нь $CAM$ гурвалжны дундаж шугам болно. Иймээс $p=21$. $AE=x=AD$, $CE=y=CF$, $BF=z=BD$ гэвэл
$$2x+2y+2z=2p\Rightarrow x+y+z=p,$$
$$x=p-(y+z)=p-a,\quad z=p-(x+y)=p-b.$$
$AOD$, $BOD$ гурвалжнуудаас
$$\tg\dfrac{A}{2}\cdot\tg\dfrac{B}{2}=\dfrac{r}{p-a}\cdot\dfrac{r}{p-b}$$
Эндээс $(p-a)(p-b)=56$. Героны томьёо ашиглавал
$$\sqrt{21\cdot56\cdot(21-c)}=21\cdot 4\Rightarrow c=15.$$
Үлдсэн хоёр талыг
$$\left\{\begin{array}{c}
a+b=42-15\\
(21-a)(21-b)=56
\end{array}\right.$$
системээс олбол $a=14$, $b=13$ болно.
$r=4$, $AB=c$, $AC=b$, $BC=a$, $a+b+c=2p$ гэж тэмдэглэе. $CBN$ ба $CAM$ гурвалжнууд адил хажуутай тул $MN=2p$ байх бөгөөд $KL$ нь $CAM$ гурвалжны дундаж шугам болно. Иймээс $p=21$. $AE=x=AD$, $CE=y=CF$, $BF=z=BD$ гэвэл
$$2x+2y+2z=2p\Rightarrow x+y+z=p,$$
$$x=p-(y+z)=p-a,\quad z=p-(x+y)=p-b.$$
$AOD$, $BOD$ гурвалжнуудаас
$$\tg\dfrac{A}{2}\cdot\tg\dfrac{B}{2}=\dfrac{r}{p-a}\cdot\dfrac{r}{p-b}$$
Эндээс $(p-a)(p-b)=56$. Героны томьёо ашиглавал
$$\sqrt{21\cdot56\cdot(21-c)}=21\cdot 4\Rightarrow c=15.$$
Үлдсэн хоёр талыг
$$\left\{\begin{array}{c}
a+b=42-15\\
(21-a)(21-b)=56
\end{array}\right.$$
системээс олбол $a=14$, $b=13$ болно.

3. Өгөгдсөн $N_{10}$ натурал тооны хувьд $N_{10}$, $N_{11}$, $N_{12},\dots$ сөрөг биш бүхэл тоон дарааллыг дараах дүрмээр байгуулъя. Үүнд
- Хэрэв $N_k=0$ байвал байгуулах процессийг зогсооно;
- Хэрэв $N_k>0$ байвал $N_k-1$ тоог $$N_k-1=a_m+a_{m-1}k+a_{m-2}k^2+\dots+a_0k^m$$ Энд $a_i\in\{0,1,2,\dots,k-1\}\quad i=\overline{1,n}$ дүрсэн дээр бичээд $N_{k+1}$ тоог $$a_m+a_{m-1}(k+1)+a_{m-2}(k+1)^2+\dots+a_0(k+1)^m$$ нийлбэртэй тэнцүү гэж тодорхойлъё. Бидний сонирхож байгаа дараалал ямагт төгсгөлөг гэж батал.
Заавар Бодолт
Заавар.
Бодолт. $N_{10}$ нь аравтын тооллын системд $n+1$ оронтой тоо байг. Бүх $n+1$ урттай сөрөг биш бүхэл тоон дарааллын олонлогийг дээр цагаан толгойн эрэмбэ буюу толь бичгийн эрэмбээр эрэмбэлэе. Өөрөөр хэлбэл
$$A=(a_0,a_1,\ldots,a_n),\, B=(b_0,b_1,\ldots,b_n)$$
гэсэн дарааллын хувьд $a_i\neq b_i$ байх хамгийн бага $i$ индексийн хувьд $a_i < b_i$ бол $A \prec B$ гэе.
$$N_k=a_{k,0}k^n+a_{k,1}k^{n-1}+\dots+a_{k,n-1}k+a_{k,n}$$
бүрд $A_k=(a_{k,0},a_{k,1},\ldots,a_{k,n})$ дарааллыг харгалзуулъя. Тэгвэл $A_{k}\succ A_{k+1}$ болох нь $A_n$ дарааллын тодорхойлолтоос мөрдөн гарна. Нөгөө талаас
$$A_{10}\succ A_{11}\succ A_{12}\succ\dots$$
процесс төгсгөлгүй үргэлжлэх боломжгүй тул ямар нэг гишүүн $A_m=(0,0,\ldots,0,1)$ буюу $N_m=1$ байна.
4. Дараах системийг бод:
$$\left\{\begin{array}{c}4x^2+3y^2=1\\32x^3-6x+9y-36y^3=1\end{array}\right.$$
Заавар Бодолт
Заавар.
Бодолт. $2x=\cos t$, $\sqrt3y=\sin t$ гэсэн орлуулга хийж болох нь эхний тэгшитгэлээс харагдаж байна $(-\pi\le t\le\pi)$.
$$4\cos^3t-3\cos t+3\sqrt3\sin t-4\sqrt3\sin^3t=1$$
буюу
$$\cos 3t+\sqrt3\sin 3t=1\Leftrightarrow \dfrac12\cos3t+\dfrac{\sqrt3}{2}\sin3t=\dfrac12$$
болно. Эндээс
$$\sin\left(3t+\dfrac{\pi}{6}\right)=\dfrac12\Leftrightarrow 3t+\dfrac{\pi}{6}=(-1)^k\arcsin\dfrac{1}{2}+\pi k\Leftrightarrow$$
$$t=[(-1)^k-1]\dfrac{\pi}{18}+\dfrac{\pi k}{3},~-\pi\le t\le\pi$$
тул
$$-18\le(-1)^k-1+6k\le 18\Rightarrow k=0,\pm1,\pm2,3$$
байна. Эдгээр утгуудыг анхны орлуулгад тавиад тэгшитгэлийн бүх 6 шийдийг олно.
5. $n\ge32$ үед $2,3,\dots,n$ тоонуудыг дурын аргаар хоёр бүлэгт хуваахад $a\cdot b=c$ байх $a$, $b$, $c$ тоонууд ядаж нэг бүлгээс нь олдоно гэж батал ($a=b$ байж болно).
Заавар Бодолт
Заавар.
Бодолт. Эсрэгээс нь бодлогын нөхцөлийг хангадаггүй хуваалт олдоно гэж үзье.
$$A\cup B=\{2,3,\ldots,32\}$$
$2\in A$ гэвэл $4\in B$, $16\in A$. Иймээс $2\cdot 16=32\in B$. Одоо $8$ гэсэн тоо $A$, $B$-ийн алинд ч харъяалагдахгүй гэдгийг харахад төвөгтэй биш юм.
6. Хавтгай дээр $O$ цэгт төвтэй тойрог, энэ тойргийн гадна орших $S$ цэг хоёр өгөгджээ. $P$ нь өгөгдсөн тойрогт татсан $SP$ шүргэгчийн шүргэлтийн цэг; $Q$ нь $P$ цэгээс $OS$ хэрчим дээр буулгасан перпендикулярын суурь байг. $PQ$ хэрчим дээр дурын $T$ цэг аваад тойрог, $ST$ шулуун хоёрын огтлолцлын цэгүүдийг $A$, $B$ гэж тэмдэглэв. $\measuredangle AQT=\measuredangle TQB$ байхыг батал.
Заавар Бодолт
Заавар.
Бодолт. 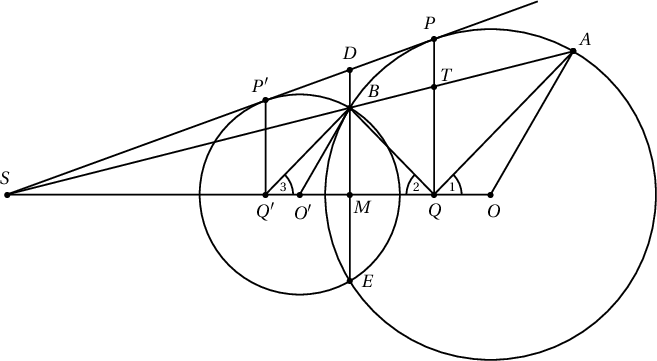 $S$ төвтэй $A\to B$ төсөөг авч үзье. Өгөгдсөн тойрог энэ төсөөгөөр $O'$ төвтэй, $PS$ шулууныг $P'$ цэгт шүргэсэн тойрогт бууна.
$$DE\parallel PQ\parallel P'Q'$$
тул огтлогч ба шүргэгчийн тухай теорем ёсоор
$$PD^2=DB\cdot DE=DP'^2\Rightarrow PD=P'D$$
Эндээс $QM=MQ'$. Иймээс $QBQ'$ адил хажуут гурвалжин болох тул түүний суурийн өнцгүүд тэнцүү
$$\angle 2=\angle 1,\quad \angle 1=\angle 3$$
байх нь илэрхий тул $\angle 2=\angle 1$. Эндээс бодлогын дүгнэлт үнэн болох нь харагдаж байна.
$S$ төвтэй $A\to B$ төсөөг авч үзье. Өгөгдсөн тойрог энэ төсөөгөөр $O'$ төвтэй, $PS$ шулууныг $P'$ цэгт шүргэсэн тойрогт бууна.
$$DE\parallel PQ\parallel P'Q'$$
тул огтлогч ба шүргэгчийн тухай теорем ёсоор
$$PD^2=DB\cdot DE=DP'^2\Rightarrow PD=P'D$$
Эндээс $QM=MQ'$. Иймээс $QBQ'$ адил хажуут гурвалжин болох тул түүний суурийн өнцгүүд тэнцүү
$$\angle 2=\angle 1,\quad \angle 1=\angle 3$$
байх нь илэрхий тул $\angle 2=\angle 1$. Эндээс бодлогын дүгнэлт үнэн болох нь харагдаж байна.
