ММО-38, 8-р анги

Монголын математикийн 38-р олимпиад, 8-р анги, 2002 он.   

Бодлогын тоо: 6    Хугацаа: 540 мин

1. Робот 1 м-ээс бага зайд байгаа зүйлийг харах бөгөөд нэг удаад 1 м алхам хийнэ. Түүнийг 1 алхам хийсний дараа түүнд "барианд ойртож байна" эсвэл "барианд ойртохгүй байна" гэж хэлж өгнө. Тэгвэл робот барианд ойртохгүй байгаа тохиолдолд алдаагаа засах замаар 38.2002 м зайд байгаа барианд 62 алхамын дараа ямагт хүрч чадах уу? (Робот бариагаа харсан үед түүнийг хүрсэн гэж үзнэ)

Заавар Бодолт
Заавар.

Бодолт. Барианд төвтэй 1 ба 38.2002 радиустай тойргууд зуръя. Тэгэхэд $A$ нь роботын анхны байрлал болно. Робот анх $A$ цэгт татсан шүргэгчийн дагуу хөдлөхөд тойргийн гадна ихдээ 6 алхам хийх юм. Үүний дараа $AO$ чиглэлд 38 алхам хийж бариаг харж чадах тул 44 алхамын дараа бариаг харна (хүрч чадна). Хэрэв анх шүргэгчийн дагуу биш дурын чиглэлд алхсан бол тойргийн гадна ихдээ 4 алхам хийнэ.
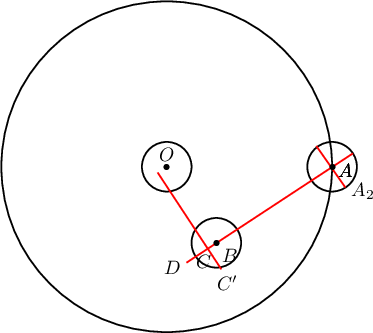Тойрог дотор алхах $AB+BO$ замуудаас хамгийн урт зам нь $ABO$ тэгш өнцөгт адил хажуут гурвалжин байх явдал. Иймд $\overline{AB}=27.01$ болох тул 28 дахь алхамын дараа барианаас холдоно ($D$ цэгт ирнэ). Буцаж 1 алхам хийж $C$ цэгт ирээд $CC'$ чиглэлд алхам хийх шаардлагагүй ($AA_2$ нь холдох байсан). Үүний дараа барианд ойртох чиглэлд 27 алхам хийхэд бариаг харна. Иймд $4+28+1+27=60$ алхамын дараа барианд хүрч чадна (харж чадна).

2. $a_n\le a_{n-1}\le\dots\le a_1$ нөхцлийг хангах $\overline{a_na_{n-1}\dots a_1}$ гэсэн $n$ оронтой тоог "буурашгүй" тоо гэе. Аливаа натурал $n$-ийн хувьд $A^2=\overline{a_na_{n-1}\dots a_1}$ байх $A^2$ ба $A$ нь "буурашгүй" байх $A$ тоо олдох уу?

3. $BC\ne CA$ байх $ABC$ гурвалжны $A,B,C$ оройн дотоод өнцгийн биссектрисийн суурь харгалзан $L_1,L_2,L_3$, $AB$ талд татсан медианы суурь $M_3$, өндрийн суурь $H_3$ болог. Хэрэв багтсан тойргийн $AB$ талтай шүргэлцсэн цэг $D$, $H_3M_3$ хэрчмийг таллан хуваавал $S_{\Delta L_1L_2L_3}=S_{\Delta CL_1L_2}$ гэж батал.

4. $\{a_n\}$ дараалал $a_1=1$, $a_2=38$ ба $n\ge1$ үед $a_{n+2}=a_{n+1}+a_n$ рекуррент харьцаагаар тодорхойлогджээ. $4\mid n$ бол $a_n-37$ тооны анхны тоон хуваагч бүр нь $a_{n+1}-36$ тоог хуваана гэж батал.

5. Үржвэр нь яг 4 ялгаатай анхны тоон хуваагчтай байх 163 ялгаатай натурал тоо өгөгджээ. Тэдгээрээс үржвэр нь бүхэл тооны 3 зэрэгт байх 3 тоог сонгон авч болно гэж батал.

6. $ABCD$ гүдгэр 4 өнцөгтийн диагоналиуд нь $M$ цэгт огтлолцоно. $ACD$ єнцгийн биссектрис $AB$ талын үргэлжлэлийг $A$ оройн талд $K$ цэгт огтлов. Хэрэв $MA\cdot MC+MA\cdot CD=MB\cdot MD$ бол $\angle BKC=\angle BDC$ гэж батал.