ММО-17, 10-р анги
Бодлогын тоо: 6 Хугацаа: 540 мин
1. 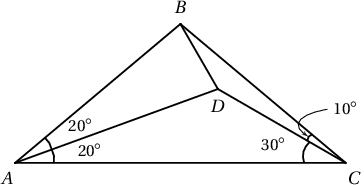 Зургаас $\angle DBC$-г ол.
Зургаас $\angle DBC$-г ол.

Заавар Бодолт
Заавар.
Бодолт. $E$ нь $B$ оройгоос буулгасан өндрийн $DC$-тай огтлолцсон цэг болог.
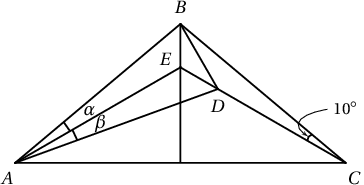 $\angle B=100^\circ$ тул $\angle ABE=50^\circ$. $ADC$ гурвалжны гадаад өнцөг болох $\angle EDA=50^\circ$, $\alpha=\beta=10^\circ$ тул $\triangle ABE=\triangle AED$. Иймд $|AB|=|AD|$ болох тул $ABD$ нь адил хажуут гурвалжин учраас
$$\angle ABD=\dfrac{180^\circ-20^\circ}{2}=80^\circ.$$
Эндээс $\angle DBC=100^\circ-80^\circ=20^\circ$.
$\angle B=100^\circ$ тул $\angle ABE=50^\circ$. $ADC$ гурвалжны гадаад өнцөг болох $\angle EDA=50^\circ$, $\alpha=\beta=10^\circ$ тул $\triangle ABE=\triangle AED$. Иймд $|AB|=|AD|$ болох тул $ABD$ нь адил хажуут гурвалжин учраас
$$\angle ABD=\dfrac{180^\circ-20^\circ}{2}=80^\circ.$$
Эндээс $\angle DBC=100^\circ-80^\circ=20^\circ$.

2. Дараах хоёр тооны аль нь их вэ?
$a=\sqrt[60]{2}$, $b=\sqrt[60]{3}$ бол $a^b$, $b^a$.
$a=\sqrt[60]{2}$, $b=\sqrt[60]{3}$ бол $a^b$, $b^a$.
Заавар Бодолт
Заавар.
Бодолт. $x=a^b=\sqrt[60]{2}^{\sqrt[60]{3}}$, $y=b^a=\sqrt[60]{3}^{\sqrt[60]{2}}$ гэж тэмдэгдэе.
$$x^{\sqrt[60]{3^{59}}}=\big({\sqrt[60]{2}}^{\sqrt[60]{3}}\big)^{\sqrt[60]{3^{59}}} =\sqrt[60]{2^{3}}=\sqrt[60]{8}$$
$$y^{\sqrt[60]{2^{59}}}=\big({\sqrt[60]{3}}^{\sqrt[60]{2}}\big)^{\sqrt[60]{2^{59}}}=\sqrt[60]{3^{2}}=\sqrt[60]{9}.$$
Иймд $x^{\sqrt[60]{3^{59}}} < y^{\sqrt[60]{2^{59}}}$ болно. Иймд $x < y$ буюу $a^b < b^a$.
3. Нэгэн дугуй ширээг тойрон 1981 хүүхэд, 1921 том хүн суужээ. Зэрэгцэн суусан хүүхдийн хосын тооноос, зэрэгцэн суусан томчуудын тоог хасахад 60 болохыг батал.
Заавар Бодолт
Заавар.
Бодолт. Зэрэгцэж суусан хүүхдүүдийн хосын тоог $N$, зэрэгцэж суусан томчуудын хосын тоог $M$ гэе. Дурын нэг хүүхдийг бэхлээд цагийн зүүний эсрэг чиглэлд хүүхдээс том хүнд гэсэн шилжилтийг тоолбол $1981-N$, том хүнээс хүүхдэд гэсэн шилжилт нь $1921-M$ болно.
Одоо $1981-N=1921-M$ болохыг баталъя. Хүүхдээс хүүхэд, том хүнээс том хүнд гэсэн шилжилтийг үл тооцвол дээрх тоололтоор $x\to T \to x\to T \to \cdots \to T\to x $ тул $x\to T, T\to x$ гэсэн шилжилтүүдийн тоо тэнцүү байна. Иймд $1981-N=1921-M$ буюу $N-M=60$
Одоо $1981-N=1921-M$ болохыг баталъя. Хүүхдээс хүүхэд, том хүнээс том хүнд гэсэн шилжилтийг үл тооцвол дээрх тоололтоор $x\to T \to x\to T \to \cdots \to T\to x $ тул $x\to T, T\to x$ гэсэн шилжилтүүдийн тоо тэнцүү байна. Иймд $1981-N=1921-M$ буюу $N-M=60$
4. $(\overline{abc})^2=(a+b+c)^5$ нөхцлийг хангадаг бүх 3 оронтой тоог ол.
Заавар Бодолт
Заавар.
Бодолт. Өгсөн нөхцөл ёсоор $\overline{abc}=\left(\dfrac{\overline{abc}}{(a+b+c)^2}\right)^5$ ба $\left(\dfrac{\overline{abc}}{(a+b+c)^2}\right)^2=a+b+c$
тул $\dfrac{\overline{abc}}{(a+b+c)^2}$ нь бүхэл тоо байна. $4^5>1000$ учраас $\overline{abc}=3^5=243$ байх ганцхан боломж байна.
5. $a>2$ бодит тоо бол $\sin\dfrac{\pi}{a}>\dfrac{3}{\sqrt{a^2+9}}$ тэнцэтгэл бишийг батал.
Заавар Бодолт
Заавар.
Бодолт. $a>0$ үед $0<\dfrac{\pi}{a} < \dfrac{\pi}{2}$ болох учраас $\tan{\dfrac{\pi}{a}} > \dfrac{\pi}{a}$ байдаг. Эндээс $\tan{\dfrac{\pi}{a}} > \dfrac{3}{a}$ болно. Иймд $\tan^2{\dfrac{\pi}{a}} > \dfrac{9}{a^2}$ буюу $a^2\sin^2{\dfrac{\pi}{a}}>9-9\cdot \sin^2{\dfrac{\pi}{a}}$ болж батлах зүйл батлагдав.
6. $x^2+xy-y^2=1$ тэгшитгэлийн $x>100$, $y>100$ байх ядаж нэг бүхэл тоон шийдийг ол.
Заавар Бодолт
Заавар.
Бодолт. Тэгшитгэлийнхээ хэлбэрийг хялбар болгох зорилгоор $x=u-v$, $y=2v$ гэж орлуулбал, манай тэгшитгэл $u^2-5v^2=1$ хэлбэртэй болно. $u=9$, $v=4$ нь энэ тэгшитгэлийн нэг шийд мөн.
Одоо энэ шийдийг томсгох асуудлыг авч үзье. $n$ нь натурал тоо бол $(9+4\sqrt{5})^n=\displaystyle{\sum_{k=0}^n} 9^{n-k}(4\sqrt{5})^k \text{C}{}^{k}_{n}=a_n+b_n\sqrt{5}$ хэлбэртэйгээр бичиж болдог. Энд $a_n, b_n$ нь натурал тоонууд. Тэгвэл $(9-4\sqrt{5})^n=a_n-b_n\sqrt{5}$ байх юм. Эндээс натурал тоо $n$ бүрийн хувьд $u=a_n$, $u=b_n$ нь $u^2-5v^2=1$ тэгшитгэлийн шийд болно. Одоо $x>100$, $y>100$ байхаар $n$-ийг авч үзэхэд асуудал дуусна. $(9+4\sqrt{5})^3=2889+1292\sqrt{5}$ учраас $y=2v=2584$, $x=u-v=1597$ нь манай тэгшитгэлийн шийд мөн.
Одоо энэ шийдийг томсгох асуудлыг авч үзье. $n$ нь натурал тоо бол $(9+4\sqrt{5})^n=\displaystyle{\sum_{k=0}^n} 9^{n-k}(4\sqrt{5})^k \text{C}{}^{k}_{n}=a_n+b_n\sqrt{5}$ хэлбэртэйгээр бичиж болдог. Энд $a_n, b_n$ нь натурал тоонууд. Тэгвэл $(9-4\sqrt{5})^n=a_n-b_n\sqrt{5}$ байх юм. Эндээс натурал тоо $n$ бүрийн хувьд $u=a_n$, $u=b_n$ нь $u^2-5v^2=1$ тэгшитгэлийн шийд болно. Одоо $x>100$, $y>100$ байхаар $n$-ийг авч үзэхэд асуудал дуусна. $(9+4\sqrt{5})^3=2889+1292\sqrt{5}$ учраас $y=2v=2584$, $x=u-v=1597$ нь манай тэгшитгэлийн шийд мөн.