ММО-14, 10-р анги
Бодлогын тоо: 6 Хугацаа: 540 мин
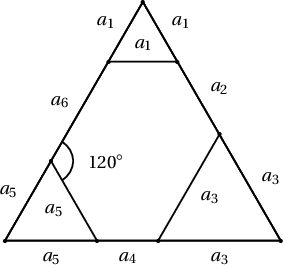
1. Гүдгэр 6 өнцөгтийн дотоод өнцгүүд тэнцүү бол
$$S\ge\dfrac{\sqrt3}{2}(a_1a_2+a_3a_4+a_5a_6)$$
болохыг батал. Энд $S$ нь зургаан өнцөгтийн талбай; $a_1,\dots,a_6$ дараалсан талууд болно.
Заавар Бодолт
Заавар.
Бодолт. Бүх өнцөгүүд нь $120^\circ$ ба $a_1+a_2=a_4+a_5$, $a_3+a_4=a_1+a_6$ болохыг харахад төвөгтэй биш юм.
Эндээс $a_5=a_1+a_2-a_4$, $a_6=a_3+a_4-a_1$ болно.
 \begin{align*}
S&=\dfrac{\sqrt3}{4}(a_1+a_2+a_3)^2-\dfrac{\sqrt3}{4}a_1^2-\dfrac{\sqrt3}{4}a_3^2-\dfrac{\sqrt3}{4}a_5^2\\
&=\dfrac{\sqrt3}{4}\big(2a_1a_2+2a_1a_3+2a_2a_3+a_3^2-(a_1+a_2-a_4)^2\big)\\
&=\dfrac{\sqrt{3}}{4}(2a_1a_3+2a_2a_3+a_3^2-a_1^2-a_2^2-a_4^2+2a_1a_4+2a_2a_4)\\
\end{align*}
Нөгөө талаас
\begin{align*}
\dfrac{\sqrt3}{2}(a_1a_2+a_3a_4+a_5a_6)&=\dfrac{\sqrt{3}}{2}\big(a_1a_2+a_3a_4+(a_1+a_2-a_4)(a_3+a_4-a_1)\big)\\
&=\dfrac{\sqrt{3}}{2}(a_1a_3+a_1a_4-a_1^2+a_2a_3+a_2a_4-a_4^2+a_1a_4)\\
&=\dfrac{\sqrt{3}}{4}(2a_1a_3+2a_1a_4-2a_1^2+2a_2a_3+2a_2a_4-2a_4^2+2a_1a_4)\\
\end{align*}
тул өгсөн тэнцэтгэл биш
$$a_1^2+a_3^2+a_4^2\geqslant a_2^2+2a_1a_4$$
тэнцэтгэл бишийг батлахад шилжинэ. Тэгш хэмтэй тул $a_3$-ийг хамгийн урт тал буюу $a_3^2\geqslant a_2^2$ гэж үзэж болно. Түүнчлэн $a_1^2+a_4^2\geqslant 2a_1a_4$ болохыг тооцвол батлах тэнцэтгэл биш батлагдав. Тэнцэлдээ хүрэх нөхцөл нь $$a_1=a_2=a_3=a_4=a_5=a_6$$
байна.
\begin{align*}
S&=\dfrac{\sqrt3}{4}(a_1+a_2+a_3)^2-\dfrac{\sqrt3}{4}a_1^2-\dfrac{\sqrt3}{4}a_3^2-\dfrac{\sqrt3}{4}a_5^2\\
&=\dfrac{\sqrt3}{4}\big(2a_1a_2+2a_1a_3+2a_2a_3+a_3^2-(a_1+a_2-a_4)^2\big)\\
&=\dfrac{\sqrt{3}}{4}(2a_1a_3+2a_2a_3+a_3^2-a_1^2-a_2^2-a_4^2+2a_1a_4+2a_2a_4)\\
\end{align*}
Нөгөө талаас
\begin{align*}
\dfrac{\sqrt3}{2}(a_1a_2+a_3a_4+a_5a_6)&=\dfrac{\sqrt{3}}{2}\big(a_1a_2+a_3a_4+(a_1+a_2-a_4)(a_3+a_4-a_1)\big)\\
&=\dfrac{\sqrt{3}}{2}(a_1a_3+a_1a_4-a_1^2+a_2a_3+a_2a_4-a_4^2+a_1a_4)\\
&=\dfrac{\sqrt{3}}{4}(2a_1a_3+2a_1a_4-2a_1^2+2a_2a_3+2a_2a_4-2a_4^2+2a_1a_4)\\
\end{align*}
тул өгсөн тэнцэтгэл биш
$$a_1^2+a_3^2+a_4^2\geqslant a_2^2+2a_1a_4$$
тэнцэтгэл бишийг батлахад шилжинэ. Тэгш хэмтэй тул $a_3$-ийг хамгийн урт тал буюу $a_3^2\geqslant a_2^2$ гэж үзэж болно. Түүнчлэн $a_1^2+a_4^2\geqslant 2a_1a_4$ болохыг тооцвол батлах тэнцэтгэл биш батлагдав. Тэнцэлдээ хүрэх нөхцөл нь $$a_1=a_2=a_3=a_4=a_5=a_6$$
байна.

2. $P_1,\dots,P_k$ нь $m+n$-ийг хуваадаг ялгаатай анхны тоонууд бөгөөд эдгээрээс яг $S$ ширхэг нь $n$-ийг хуваадаг бол дараах тэнцэтгэлийг батал.
$$\sum_{\{i_1,\dots,i_j\}}\left(\left[\dfrac{m+n}{P_{i_1}P_{i_2}\dots P_{i_j}}\right]-\left[\dfrac{m}{P_{i_1}P_{i_2}\dots P_{i_j}}\right]-\left[\dfrac{n}{P_{i_1}P_{i_2}\dots P_{i_j}}\right]\right)=2^{k}-2^{s}$$
Энд $\{i_1,\dots,i_j\}$ гэсэн $\{1,\dots,k\}$-ийн бүх хоосон биш дэд олонлогоор нийлбэрчилнэ.
Заавар Бодолт
Заавар.
Бодолт. $p_1,p_2,\ldots,p_s$ нь $n$-ийг хуваадаг гэж үзье. Тэгвэл эдгээр нь $m+n$-ийг хуваадаг учир $m$-ийг бас хуваана.
$$\dfrac{m+n}{p_{i_1}p_{i_2}\ldots p_{i_j}}=x, \dfrac{m}{p_{i_1}p_{i_2}\ldots p_{i_j}}=y, \dfrac{n}{p_{i_1}p_{i_2}\ldots p_{i_j}}=z$$
гэсэн тэмдэглэл хийвэл
$$x-y-z=0$$
эндээс
$$[x]+\{x\}-[y]-\{y\}-[z]-\{z\}=0,$$
$\{y\}+\{z\}-\{x\}$ нь бүхэл утга авдаг бол $0,1$-ээс өөр утга авах боломжгүй. Иймд нэг бол
$$[x]-[y]-[z]=1$$
эсвэл
$$[x]-[y]-[z]=0.$$
Өгөгдсөн нийлбэр нь
$$C_k^1+C_k^2+\dots+C_{k}^k=2^k-1$$
нэмэгдэхүүнтэй. Иймд нийлбэрийн утга нь $2^k-1$-ээс хэтрэхгүй юм. $p_{i1}\ldots p_{ij}$ нь бүгд $p_1,p_2,\ldots,p_s$-ээс бүрдсэн тийм нэмэгдэхүүн бүр $0$-тэй тэнцүү байна. Учир нь
$$\left[\dfrac{m+n}{p_{i_1}p_{i_2}\ldots p_{i_j}}\right]-\left[\dfrac{m}{p_{i_1}p_{i_2}\ldots p_{i_j}}\right]-\left[\dfrac{n}{p_{i_1}p_{i_2}\ldots p_{i_j}}\right]=$$
$$=\dfrac{m+n}{p_{i_1}p_{i_2}\ldots p_{i_j}}-\dfrac{m}{p_{i_1}p_{i_2}\ldots p_{i_j}}-\dfrac{n}{p_{i_1}p_{i_2}\ldots p_{i_j}}=0$$
Ийм нэмэгдэхүүн өгөгдсөн нийлбэрт
$$C_s^1+C_s^2+\dots+C_s^s=2^s-1$$
ширхэг байна. Хэрэв $p_{i_1},\ldots,p_{i_j}$-ийн ядаж нэг нь $p_{s+1},p_{s+2},\ldots,p_k$-ийн аль нэгтэй тэнцүү бол
$\dfrac{m+n}{p_{i_1}p_{i_2}\ldots p_{i_k}}$ бүхэл $\dfrac{m}{p_{i_1}p_{i_2}\ldots p_{i_k}}$ бүхэл биш, $\dfrac{n}{p_{i_1}p_{i_2}\ldots p_{i_k}}$ бүхэл биш учир
$$\left[\dfrac{m+n}{p_{i_1}p_{i_2}\ldots p_{i_j}}\right]-\left[\dfrac{m}{p_{i_1}p_{i_2}\ldots p_{i_j}}\right]-\left[\dfrac{n}{p_{i_1}p_{i_2}\ldots p_{i_j}}\right]\neq 0$$
иймд
$$\left[\dfrac{m+n}{p_{i_1}p_{i_2}\ldots p_{i_j}}\right]-\left[\dfrac{m}{p_{i_1}p_{i_2}\ldots p_{i_j}}\right]-\left[\dfrac{n}{p_{i_1}p_{i_2}\ldots p_{i_j}}\right]=1$$
Ингэхлээр өгөгдсөн нийлбэр нь $2^k-1$ нэмэгдэхүүнтэй бөгөөд түүний яг $2^s-1$ нь $0$-тэй тэнцүү бусад нь $1$-тэй тэнцүүү юм. Иймд
$$\sum_{\{i_1,\ldots,i_j\}}\left[\dfrac{m+n}{p_{i_1}p_{i_2}\ldots p_{i_j}}\right]-\left[\dfrac{m}{p_{i_1}p_{i_2}\ldots p_{i_j}}\right]-\left[\dfrac{n}{p_{i_1}p_{i_2}\ldots p_{i_j}}\right]=(2^k-1)-(2^s-1)=2^k-2^s.$$
3. Нийлбэр нь $832$ байх ба квадратууд нь геометр прогресс үүсгэх бүх натурал тоон гурвалыг ол.
Заавар Бодолт
Заавар.
Бодолт. Олох ёстой тоонуудыг $a,b,c$ гэе. Тэгвэл $a < b < c$ гэж үзэж болно. $a^2, b^2, c^2$-геометр прогрессын хуваарийг $d$ гэе. Тэгвэл $a^2$, $b^2=a^2d$, $c^2=a^2d^2$ ба $a$, $b=a\sqrt{d}$, $c=ad$ нь мөн геометр прогресс үүсгэнэ. $d=q^2$ гэвэл $a$, $b=aq$, $c=aq^2$ ба $q>1$. Иймд
$$a+b+c=a+aq+aq^2=a(q^2+q+1)=832,$$
$q$ нь рационал тоо байж болох учир $q=\dfrac{m}{n}$, $(m,n)=1$, $m>n$ гэж үзье. Энд $m,n\in N$. Тэгвэл
$$a\left(\dfrac{m^2}{n^2}+\dfrac{m}{n}+1\right)=a\cdot \dfrac{m^2+mn+n^2}{n^2}=832\qquad(1)$$
Гэтэл $(m^2+mn+n^2,n)=1$ тул $(m^2+mn,n^2)=1$ буюу $(m^2+mn+n^2,n^2)=1$. Иймд $a=n^2S$, $S\in\mathbb N$ дүрсээр бичигдэнэ.
Тэгвэл $(1)$-ийг $S(m^2+mn+n^2)=832=2^6\cdot 13$ гэж бичиж болно. $(n,m)=1$ гэж үзсэн учраас $m^2+mn+n^2$ сондгой тоо юм. Иймд $m^2+mn+n^2=13$, $m,n\le 13$, $m>n$ болохыг анхаарвал үүний шийд зөвхөн $m=3$, $n=1$. Ийм учраас $q=\dfrac{m}{n}=3$ ба $a=2^6=64$, $b=64\cdot 3=192$, $c=192\cdot 3=576$, $(64,192,576)$.
Тэгвэл $(1)$-ийг $S(m^2+mn+n^2)=832=2^6\cdot 13$ гэж бичиж болно. $(n,m)=1$ гэж үзсэн учраас $m^2+mn+n^2$ сондгой тоо юм. Иймд $m^2+mn+n^2=13$, $m,n\le 13$, $m>n$ болохыг анхаарвал үүний шийд зөвхөн $m=3$, $n=1$. Ийм учраас $q=\dfrac{m}{n}=3$ ба $a=2^6=64$, $b=64\cdot 3=192$, $c=192\cdot 3=576$, $(64,192,576)$.
4. Бодит тоон олонлог дээр тодорхойлогдсон бөгөөд дурын бодит тоо $a,b$-ийн хувьд
$$f(a+b)=\dfrac{f(a)+f(b)}{1+f(a)\cdot f(b)}$$
нөхцөлийг хангах бүх тэгш функц $f(x)$-үүдийг ол.
Заавар Бодолт
Заавар.
Бодолт. $a=2x$, $b=-x$ үед
$$f(x)=\dfrac{f(2x)+f(-x)}{1+f(2x)f(-x)}=\dfrac{f(2x)+f(x)}{1+f(2x)f(x)}\Rightarrow$$
$$1+f(2x)f(x)\neq0,\quad f(2x)(f^2(x)-1)=0.$$
$a=b=x$ үед
$$f(2x)=\dfrac{2f(x)}{1+f^2(x)}$$
тул
$$\dfrac{2f(x)}{1+f^2(x)}[f^2(x)-1]=0\Rightarrow f(x)(f^2(x)-1)=0$$
болно. Иймд $f(x)=0$, эсвэл $f(x)=1$, эсвэл $f(x)=-1$. Одоо $0$, $1$, $-1$ утгуудыг бүгдийг нь авдаг $f(x)$ функц олдохгүй гэж баталъя. Хэрэв тийм $f(x)$ функц олддог бол түүний хувьд $f(a_0)=1$, $f(b_0)=-1$ байдаг $a_0$, $b_0$ цэгүүд олдоно. Гэтэл $1+f(a_0)f(b_0)\neq 0$ байх ёстой билээ. Иймд $f(x)$ нь нэг бол $0,1$ эсвэл $0,-1$ утгуудыг л авдаг байх ёстой. $f(x)$ нь $0; 1$ утгуудыг авдаг байг. Тэгвэл
$$f(x_1)=0, f(x_1+\Delta x)=f(x_2)=1$$
байх $x_1, x_2=x_1+\Delta x$ цэгүүд олдоно. Гэтэл $f(\Delta x)\neq-1$ тул
$$f(x_1)=f(x_2-\Delta x)=\dfrac{f(x_2)+f(-\Delta x)}{1+f(x_2)f(-\Delta x)}=\dfrac{1+f(\Delta x)}{1+f(\Delta x)}=1$$
Энэ нь бидний $f(x_1)=0$ гэж авсанд харшилна. Үүнтэй адилаар $f(x)$ нь $0;-1$ утгуудыг авдаг гэвэл
$f(x_1)=0$, $f(x_2)=-1$ ба $f(\Delta x)\neq 1$ тул
$$f(x_1)=f(x_2-\Delta x)=\dfrac{f(x_2)+f(\Delta x)}{1+f(x_2)f(\Delta x)}=\dfrac{-1+f(\Delta x)}{1-f(\Delta x)}=-1$$
болж бас авсан нөхцөлд харшилна. Иймд бодлогын нөхцөлийг зөвхөн $f_1(x)=0$, $f_2(x)=1$, $f_3(x)=-1$ функцүүд хангана.
5. $\alpha_1,\dots,\alpha_n$ нь хос хосоороо ялгаатай бөгөөд $0\le\alpha_i\le\pi$, $i=1,\dots, n$ байх өнцгүүд, $n$ сондгой натурал тоо бол
$$(\sin\alpha_1+\dots+\sin\alpha_n)^2+(\cos\alpha_1+\dots+\cos\alpha_2)^2\ge 1$$
тэнцэтгэл бишийг батал.
Заавар Бодолт
Заавар.
Бодолт. $n=1$ үед $\sin^2\alpha+\cos^2\alpha=1$ учир тэнцэтгэл биш үнэн. Иймд хойшид $n\ge 3$ гэж үзье. Хэрэв
$$\sin\alpha_1+\sin\alpha_2+\dots+\sin\alpha_n\ge 1$$
байвал тэнцэтгэл биш илэрхий үнэн. Иймд
$$\sin\alpha_1+\sin\alpha_2+\dots+\sin\alpha_n < 1\qquad(1)$$
гэж үзье. $(1)$ нөхцөл биелж байхын тулд
$\left[\dfrac{\pi}{6};\dfrac{5\pi}{6}\right]$
интервалд өгөгдсөн $\alpha_1,\ldots,\alpha_n$ өнцгүүдээс нэгээс ихгүй нь харъяалагдаж болно. Хэрэв энэ интервалд харъяалагддаг өнцөг байдаг бол
түүнийг $\alpha_m$ гэе. Тэгвэл $\alpha_m\neq\dfrac{\pi}{2}$. Ингэхлээр $\alpha_m$-ээс бусад бүх өнцөг нь $\left[0;\dfrac{\pi}{6}\right]$, $\left[\dfrac{5\pi}{6},\pi\right]$ харъяалагдах ёстой. Тэдгээрийн хувьд $0\le \sin\alpha_i\le\dfrac{1}{2}$, $i\neq m$. Харин $\dfrac12\le\sin\alpha_m<1$. Нөгөө талаас
\begin{align*}
\cos\alpha_1+\dots+\cos\alpha_n&=1-2\sin^2\dfrac{\alpha_1}{2}+\dots+1-2\sin^2\dfrac{\alpha_n}{2}\\
&=n-2\left(\sin^2\dfrac{\alpha_1}{2}+\dots+\sin^2\dfrac{\alpha_n}{2}\right)
\end{align*}
Гэтэл
$$\sin^2\dfrac{\alpha_i}{2}=\dfrac{1-\cos\alpha_i}{2}=\dfrac{1-\sqrt{1-\sin^2\alpha_i}}{2}\le\dfrac{1-\sqrt{1-\dfrac{1}{4}}}{2}=\dfrac{2-\sqrt{3}}{4}, i\neq m$$
ба
$$\sin^2\dfrac{\alpha_m}{2}=\dfrac{1-\sqrt{1-\sin^2\alpha_m}}{2}<\dfrac{1}{2}$$
Иймд
$$\sin^2\dfrac{\alpha_1}{2}+\dots+\sin^2\dfrac{\alpha_n}{2}<\dfrac{2-\sqrt{3}}{4}(n-1)+\dfrac12=\dfrac{2n-\sqrt{3}(n-1)}{4}$$
ба
$$\cos\alpha_1+\dots+\cos\alpha_m=n-2\cdot\left(\sin^2\dfrac{\alpha_1}{2}+\dots+\sin^2\dfrac{\alpha_n}{2}\right)>{}$$
$${}>n-2\cdot\dfrac{2n-\sqrt{3}(n-1)}{4}=\dfrac{\sqrt{3}(n-1)}{2}$$
буюу
$$\cos\alpha_1+\dots+\cos\alpha_n > \dfrac{\sqrt{3}(n-1)}{2}$$
$n\ge 3$ үед $\dfrac{\sqrt{3}(n-1)}{2} > 1$ учир
$$\cos\alpha_1+\dots+\cos\alpha_n>1$$
Ийм учир $(1)$ нөхцөл биелэх үед
$$\cos\alpha_1+\dots+\cos\alpha_n>1$$
учраас батлах ёстой тэнцэтгэл биш үнэн байна.
6. Зөв гурвалжин дотор дурын $O$ цэг авчээ. Энэ цэгээс оройнууд хүртэлх зайнуудын нийлбэр, энэ цэгээс талууд хүртэлх зайнуудын нийлбэрийг 2 дахин авснаас багагүй гэдгийг батал. Хэдийд тэнцэл биелэх вэ?
Заавар Бодолт
Заавар.
Бодолт. $AH=h$, $AO=a$, $BO=b$, $CO=c$, $OM=\ell_a$, $ON=\ell_b$, $OP=\ell_c$ гэж тэмдэглэе.
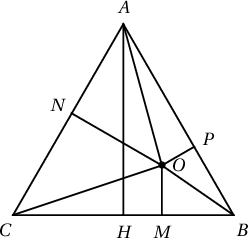 $$\dfrac{S_{BOC}}{S_{ABC}}=\dfrac{\ell_a}{h},\quad\dfrac{S_{AOC}}{S_{ABC}}=\dfrac{\ell_b}{h},\dfrac{S_{AOB}}{S_{ABC}}=\dfrac{\ell_c}{h}$$
Иймд
$$\dfrac{\ell_a}{h}+\dfrac{\ell_b}{h}+\dfrac{\ell_c}{h}=\dfrac{S_{BOC}+S_{AOC}+S_{AOB}}{S_{ABC}}=1$$
буюу
$$\ell_a+\ell_b+\ell_c=h$$
Нөгөө талаас $h\le a+\ell_a$, $h\le b+\ell_b$, $h\le c+\ell_c$. Иймд
$$a+b+c\ge 3h-(\ell_a+\ell_b+\ell_c)=2(\ell_a+\ell_b+\ell_c).$$
$O$ цэг өгөгдсөн зөв гурвалжны төвтэй давхцах үед тэнцэлдээ хүрнэ.
$$\dfrac{S_{BOC}}{S_{ABC}}=\dfrac{\ell_a}{h},\quad\dfrac{S_{AOC}}{S_{ABC}}=\dfrac{\ell_b}{h},\dfrac{S_{AOB}}{S_{ABC}}=\dfrac{\ell_c}{h}$$
Иймд
$$\dfrac{\ell_a}{h}+\dfrac{\ell_b}{h}+\dfrac{\ell_c}{h}=\dfrac{S_{BOC}+S_{AOC}+S_{AOB}}{S_{ABC}}=1$$
буюу
$$\ell_a+\ell_b+\ell_c=h$$
Нөгөө талаас $h\le a+\ell_a$, $h\le b+\ell_b$, $h\le c+\ell_c$. Иймд
$$a+b+c\ge 3h-(\ell_a+\ell_b+\ell_c)=2(\ell_a+\ell_b+\ell_c).$$
$O$ цэг өгөгдсөн зөв гурвалжны төвтэй давхцах үед тэнцэлдээ хүрнэ.
