ММО-12, 10-р анги
Бодлогын тоо: 8 Хугацаа: 540 мин
1. $3\sqrt{x^3+a^3}=2x^2+(1-2a)x+a(1+2a)$ тэгшитгэл ядаж нэг бодит $x$ шийдтэй байх $a$ параметрийн хамгийн их ба хамгийн бага утгыг ол.
Заавар Бодолт
Заавар.
Бодолт. $x^3+a^3= (x + a) (x^2 - ax + a^2)\ge 0$ байх ёстой тул $x + a\ge 0$ болно. Учир нь
$$x^2-ax+a^2=\left(x-\dfrac{a}{2}\right)^2+\dfrac{3a^2}{4}\ge 0$$
билээ. Иймд $x+a=u^2, x^2-ax+a^2=v^2$
орлуулга хийж болно. Тэгвэл өгсөн тэгшитгэл нь
$$3uv = u^2 + 2v^2\qquad(1)$$
хэлбэртэй болно. $u=0$ байх зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь $v=0$ бөгөөд энэ үед харгалзах шийд нь $x=a=0$ болно. Бусад шийдийг олохын тулд $u\neq 0$ гэж үзэж болох ба $(1$) тэгшитгэлийн 2 талыг $u$-д хувааж $t=\dfrac{v}{u}$ орлуулга хийвэл
$$2t^2-3t + 1=0\qquad(2)$$
болно. Үүний шийд нь $t_1 = 1, t_2=\dfrac{1}{2}$ юм. Иймд өгөгдсөн тэгшитгэл ядаж нэг бодит шийдтэй байх зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь
$$\dfrac{x^2-ax+a^2}{x+a}=1\qquad(3)$$
эсвэл
$$\dfrac{x^2-ax+a^2}{x+a}=\dfrac{1}{4}\qquad(4)$$
тэгшитгэлүүдийн ядаж нэг нь бодит шийдтэй байх ба тэр шийд нь $x+a\ge 0$-ийг хангах явдал юм. $(3)$ тэгшитгэл бодит шийдтэй байхын тулд
$$D_1=(a+1)^2 - 4 (a^2-a)=-3a^2 + 6a+ 1\ge 0$$
буюу
$$\dfrac{3-2\sqrt{3}}{3}\le a\le\dfrac{3+2\sqrt{3}}{3}\qquad(5)$$
байх явдал юм. $a=\dfrac{3-2\sqrt{3}}{3}$ үед $(3)$ тэгшитгэл давхардсан бодит шийд $x=\dfrac{a+1}{2}=\dfrac{3-\sqrt{3}}{3}$-тэй
ба энэ үед өгсөн тэгшитгэл бодит шийдтэй.
Яг үүнтэй адилаар $a=\dfrac{3+2\sqrt{3}}{3}$ үед ч өгсөн тэгшитгэл бодит шийдтэй болохыг харуулна. $(4)$ тэгшитгэл шийдтэй байх $a$-ийн муж $(5)$ завсарт багтахыг хялбархан харуулж болно. Иймд
$$a_{\min}=\dfrac{3-2\sqrt{3}}{3}, a_{\max}=\dfrac{3+2\sqrt{3}}{3}$$
болно.
2. Хавтгайд $ABCD$ квадрат ба түүн дотор өгөгдсөн квадратын талуудтай параллел талуудтай $A_1B_1C_1D_1$ квадрат өгөгдөв.
- $A_1B_1C_1D_1$ суурьтай дурын жишүү өнцөгт параллелепипедийн дээд суурь нь $A'B'C'D'$ бол $AA'$, $BB'$, $CC'$, $DD'$ шулуунууд нэг $S$ цэгт огтлолцоно гэдгийг батал.
- $A_1B_1C_1D_1A'B'C'D'$ параллелепипедийн суурь $A_1B_1C_1D_1$ бэхлэгдээд хажуу ирмэг $|AA_1|$-ийн урт тогтмол байх үед $S$ цэгүүд огторгуйд ямар геометр байр үүсгэх вэ?
3. Дурын арифметик прогрессийн $a_{n-k}$, $a_n$, $a_{n+k}$ гурван гишүүний хувьд
\[a_{n-k}^{2^s}+a_{n+k}^{2^s}\ge 2a_n^{2^s}\]
байхыг үзүүл, энд $s$ натурал тоо. Тэнцэл хэдийд биелэх вэ?
Заавар Бодолт
Заавар.
Бодолт. Аливаа $a$, $b$ тоонуудын ба $n\in\mathbb N$ тооны хувьд
$$a^{2^n}+b^{2^n}\ge 2\cdot\left(\dfrac{a+b}{2}\right)^{2^n}$$
болохыг индункцээр баталъя. $n=1$ үед
$$\dfrac{a^2+b^2}{2}\ge\left(\dfrac{a+b}{2}\right)^2\Leftrightarrow (a-b)^2\ge 0$$
тэнцэтгэл бишийг ашиглавал
$$a^2+b^2\ge 2\cdot\left(\dfrac{a+b}{2}\right)^2$$
$n=k$ үед үнэн гээд $n=k+1$ үед баталъя.
$$a^{2^{k+1}}+b^{2^{k+1}}=(a^2)^{2^k}+(b^2)^{2^k}\ge 2\cdot \left(\dfrac{a^2+b^2}{2}\right)^{2^{k}}\ge{}$$
$${}\ge 2\cdot\left(\left(\dfrac{a+b}{2}\right)^2\right)^{2^k}=2\cdot\left(\dfrac{a+b}{2}\right)^{2^{k+1}}$$
болж батлагдав.
$a_{n-k}+a_{n+k}=2a_n$ ба өмнө баталсан тэнцэтгэл бишийг ашиглавал батлах зүйл илэрхий юм. Тэнцэлдээ хүрэх нөхцөл нь $d=0$ байна.
$a_{n-k}+a_{n+k}=2a_n$ ба өмнө баталсан тэнцэтгэл бишийг ашиглавал батлах зүйл илэрхий юм. Тэнцэлдээ хүрэх нөхцөл нь $d=0$ байна.
4. Хэрэв $f(x)$ функц дурын $x$ ба тогтмол $m$-ийн хувьд $f(x+m)=\dfrac{f(x)+1}{1-f(x)}$ функцэн тэгшитгэлд тохирдог бол түүнийг үетэй гэж батал.
Заавар Бодолт
Заавар.
Бодолт. $x\to x+m$ гэвэл
\begin{align*}
f(x+2m)&=\dfrac{f(x+m)+1}{1-f(x+m)}=\dfrac{\frac{f(x)+1}{1-f(x)}+1}{1-\frac{f(x)+1}{1-f(x)}}\\
&=\dfrac{f(x)+1+1-f(x)}{1-f(x)-f(x)-1}=-\dfrac{1}{f(x)}
\end{align*}
болно. Иймд
$$f(x+4m)=-\dfrac{1}{f(x+2m)}=f(x)$$
болно. Иймд $f(x)$ функц $4m$ үетэй болж батлагдав.
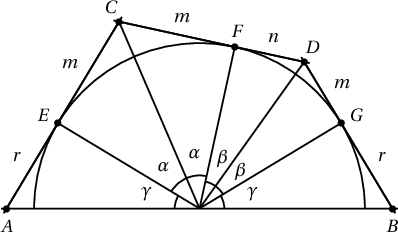
5. Урт нь үл мэдэгдэх $AB$ хэрчмийн дундаж дээр төвтэй, $|AB|$-ээс бага диаметртэй хагас тойргийг байгуулан түүнд $A$, $B$ цэгүүдээс $r$ урттай шүргэгчдийг татаж; нэгийг нь цааш $n$, нөгөөг нь $m$ урттайгаар үргэлжлүүлэн үзүүрүүдийг нь холбоход гарах хэрчим тойргийг шүргэж байсан бол хагас тойргийн радиусыг ол.
Заавар Бодолт
Заавар.
Бодолт. Өгсөн ёсоор $|AE|=|BG|=r$, $|EC|=|CF|=m$, $|FD|=|DG|=n$, $|OE|=|OF|=|OG|=R$, $\angle COF=\angle COE=\alpha$, $\angle FOD=\angle DOG=\beta$, $\angle AOE=\angle BOG=\gamma$ гэвэл $\alpha+\beta+\gamma=90^\circ$, $\tg\alpha=\dfrac{m}{r}$, $\tg\beta=\dfrac{n}{R}$, $\tg\gamma=\dfrac{r}{R}$ болно. Нөгөө талаас
$$\tg\gamma=\tg\big(90^\circ-(\alpha+\beta)\big)=\dfrac{1-\tg\alpha\cdot\tg\beta}{\tg\alpha+\tg\beta}$$
учир $\dfrac{r}{R}=\dfrac{1-\frac{mn}{R^2}}{\frac{m+n}{R}}$
буюу $R=\sqrt{rm+rn+nm}$ болно.

6. Залган бичиж тоо үүсгэхэд орсон цифр бүр нь тэгш тоотой давтагдах хэдэн тоог өгөгдсөн 11 натурал тоон дотроос сонгон авч болохыг үзүүл.
Заавар Бодолт
Заавар.
Бодолт. Өгсөн $a_1,\ldots,a_{11}$ гэсэн 11 тооноос тэдний нэг хэсгийг авч зохиосон тооны эрэмбэ ач холбогдолгүй тул тэднээс тогтох олонлогийг авч үзье. Эдгээр нь цөм $A=\{a_1,\ldots,a_{11}\}$ олонлогийн дэд олонлог болно. Тэдний тоо $2^{11}-1$ болно.
$\{a_{i_1},\ldots,a_{i_k}\}$, $1\le i_1,\ldots, i_k\le 11$ дэд олонлогийг
авбал $\overline{a_{i_1},\ldots,a_{i_k}}$ тоо нь $0,1,\ldots,9$ цифрүүдээр бичигдэнэ.
Одоо $0,1,\ldots,9$ гэсэн цифрүүдээр бичигдсэн ядаж 1 цифр тэгш тоотой ороогүй тоонуудыг мөн бүтцийн хувьд авч үзье. Цифрүүдийн байрлалыг анхаарахгүй учраас 12, 21 хоёрыг $\{1, 2\}$ олонлогтой, $123$, $132$, $321$ гурвыг $\{1, 2, 3\}$ олонлогтой тус тус адилтгаж үзнэ. Тэгвэл дээрх 10 цифрээс $2^{10}-1$ ширхэг дэд олонлогийг сонгон авч чадна. Одоо $\{a_{i_1},\ldots,a_{i_k}\}$ дэд олонлогуудыг, дараах дүрмээр $B=\{0,1,\ldots,9\}$-ийн дэд олонлогуудад харгалзуулъя. Үүнд: $a_{i_1},a_{i_2},\ldots,a_{i_k}$ тоонуудыг залгаж бичлээ гээд ямар цифрүүд сондгой удаа давтагдан орсон байна, яг тэр цифрүүдээс тогтсон дэд олонлогт $\{a_{i_1},a_{i_2},\ldots,a_{i_k}\}$ олонлогийг харгалзуулъя. Энэ харгалзаагаар $\{0,1,\ldots,9\}$-ийн ямар ч дэд олонлогт үл харгалзах $\{a_{i_1},a_{i_2},\ldots,a_{i_k}\}$ олонлог олдоно гэдгийг үзүүлье. Тэгвэл $\overline{a_{i_1},a_{i_2},\ldots,a_{i_k}}$ нь бидний эрж явсан тоо болно. Үнэндээ $A$-ийн дэд олонлогуудын тоо $2^{11}-1$ нь $B$-ийн дэд олонлогуудын тоо $2^{10}-1$-ээс их учир Дирихлейн зарчмаар ямар нэг $$A_1=\{a_{i_i},\ldots,a_{i_k}\}\neq A_2=\{a_{j_1},\ldots,a_{j_s}\}\subseteq A$$ гэсэн 2 дэд олонлог $B$-ийн нэг дэд олонлогт харгалзах болно. Тэгвэл $A_1$ ба $A_2$-ийн бүтцэд орсон цифрүүдийн тэгш сондгой нь давхцана. Иймд эдгээр 2 олонлогт давтагдан орсон цифрүүдийг орхиод хоёулангийнх нь үлдсэн тоонуудыг нэгтгэхэд энэ тооны бүрэлдэхүүнд орсон цифр бүр нь тэгш тоотой байх нь илэрхий болно (Нэгэнт $A_1\neq A_2$ учраас ийм нэгтгэл $C=\{c_{i_1},\ldots,c_{i_p}\}$ нь хоосон биш байна). Дээрх харгалзаагаар энэ тоо $B$-ийн ямар ч дэд олонлогт харгалзахгүй учир бидний эрж явсан $\overline{c_{i_1},\ldots,c_{i_p}}$ тоо болно.
Одоо $0,1,\ldots,9$ гэсэн цифрүүдээр бичигдсэн ядаж 1 цифр тэгш тоотой ороогүй тоонуудыг мөн бүтцийн хувьд авч үзье. Цифрүүдийн байрлалыг анхаарахгүй учраас 12, 21 хоёрыг $\{1, 2\}$ олонлогтой, $123$, $132$, $321$ гурвыг $\{1, 2, 3\}$ олонлогтой тус тус адилтгаж үзнэ. Тэгвэл дээрх 10 цифрээс $2^{10}-1$ ширхэг дэд олонлогийг сонгон авч чадна. Одоо $\{a_{i_1},\ldots,a_{i_k}\}$ дэд олонлогуудыг, дараах дүрмээр $B=\{0,1,\ldots,9\}$-ийн дэд олонлогуудад харгалзуулъя. Үүнд: $a_{i_1},a_{i_2},\ldots,a_{i_k}$ тоонуудыг залгаж бичлээ гээд ямар цифрүүд сондгой удаа давтагдан орсон байна, яг тэр цифрүүдээс тогтсон дэд олонлогт $\{a_{i_1},a_{i_2},\ldots,a_{i_k}\}$ олонлогийг харгалзуулъя. Энэ харгалзаагаар $\{0,1,\ldots,9\}$-ийн ямар ч дэд олонлогт үл харгалзах $\{a_{i_1},a_{i_2},\ldots,a_{i_k}\}$ олонлог олдоно гэдгийг үзүүлье. Тэгвэл $\overline{a_{i_1},a_{i_2},\ldots,a_{i_k}}$ нь бидний эрж явсан тоо болно. Үнэндээ $A$-ийн дэд олонлогуудын тоо $2^{11}-1$ нь $B$-ийн дэд олонлогуудын тоо $2^{10}-1$-ээс их учир Дирихлейн зарчмаар ямар нэг $$A_1=\{a_{i_i},\ldots,a_{i_k}\}\neq A_2=\{a_{j_1},\ldots,a_{j_s}\}\subseteq A$$ гэсэн 2 дэд олонлог $B$-ийн нэг дэд олонлогт харгалзах болно. Тэгвэл $A_1$ ба $A_2$-ийн бүтцэд орсон цифрүүдийн тэгш сондгой нь давхцана. Иймд эдгээр 2 олонлогт давтагдан орсон цифрүүдийг орхиод хоёулангийнх нь үлдсэн тоонуудыг нэгтгэхэд энэ тооны бүрэлдэхүүнд орсон цифр бүр нь тэгш тоотой байх нь илэрхий болно (Нэгэнт $A_1\neq A_2$ учраас ийм нэгтгэл $C=\{c_{i_1},\ldots,c_{i_p}\}$ нь хоосон биш байна). Дээрх харгалзаагаар энэ тоо $B$-ийн ямар ч дэд олонлогт харгалзахгүй учир бидний эрж явсан $\overline{c_{i_1},\ldots,c_{i_p}}$ тоо болно.
7. $(x+1)y$, $xy$, $(x-1)y$ нь гурвалжны өнцгүүд бол $\sin^2(x+1)y=\sin^2xy+\sin^2(x-1)y$ тэгшитгэлийг хангах $(x,y)$ хосуудыг ол.
Заавар Бодолт
Заавар.
Бодолт. Синусын теорем болон Пифагорны теоремоос $(x+1)y=\pi/2$ гэж гарна. Нөгөө талаас $(x+1)y+xy+(x-1)y=\pi$ тул $xy=\pi/3$ болно. Иймд
$(x,y)=(2,\pi/6)$ гэсэн ганц шийдтэй.
8. Огторгуйд аль ч дөрөв нь нэг хавтгайд үл орших $n$ цэг өгчээ.
- Эдгээр цэгүүд дээр оройтой бөгөөд дотроо эдгээр цэгүүдийн нэгийг нь ч агуулаагүй тетраэдрын тоо $\dfrac14C_n^3\le x\le C_n^4$ тэнцэтгэл бишийг хангахыг үзүүл.
- Эдгээр цэгүүдийн аль ч хоёрынх нь хоорондох зай тэнцүү бол $n$ хэд байх вэ?
Заавар Бодолт
Заавар.
Бодолт. Өгөгдсөн цэгүүдээс дурын гурвыг нь авч тэднийг дайруулан хавтгай татаад үлдсэн цэгүүд дотроос энэхүү хавтгайд хамгийн ойр орших цэгийг авч тетраэдр байгуулахад уг тетраэдр дотор өгөгдсөн цэгүүдээс нэг нь ч үл орно. Иймд бодлогын нөхцөлийг хангасан тетраэдрийн тоо хамгийн цөөндөө $\dfrac14C_n^3$ байна. Нийт байж болох тетраэдрийн тоо $C_n^4$ байх нь илэрхий.