Бүс, дүүрэг 2019, намар, Дунд ангийн багш
Бодлогын тоо: 4 Хугацаа: 210 мин
1. $O$ төвтэй тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн $AC$, $BD$ диагоналиуд хоорондоо перпендикуляр байв. $AB$ талын дундаж $E$, $BC$ талын дундаж $F$, $CD$ талын дундаж $G$, $AD$ талын дундаж $H$ бол
$$2(OE+OF+OG+OH)=AB+BC+CD+DA$$
гэж батал.
Заавар Бодолт
Заавар.
Бодолт. 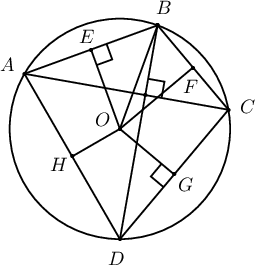
$\measuredangle EOB=\measuredangle ADB$, $\measuredangle DOG=\measuredangle DAC$, $BD\perp AC$ учир $\measuredangle ADB+\measuredangle DAC=90^\circ$. Эндээс $\measuredangle EOB=\measuredangle ODG$, $\measuredangle DOG=\measuredangle EBO$, $OB=OD$ учраас $\triangle EBO=\triangle DGO$. Иймээс $OG=EB=\dfrac{AB}{2}\Rightarrow AB=2OG$. Үүнтэй төстэйгээр $BC=2OH$, $CD=2OE$, $DA=2OF$. Эдгээрийг нэмбэл $$2(OE+OF+OG+OH)=AB+BC+CD+DA$$ болно.

$\measuredangle EOB=\measuredangle ADB$, $\measuredangle DOG=\measuredangle DAC$, $BD\perp AC$ учир $\measuredangle ADB+\measuredangle DAC=90^\circ$. Эндээс $\measuredangle EOB=\measuredangle ODG$, $\measuredangle DOG=\measuredangle EBO$, $OB=OD$ учраас $\triangle EBO=\triangle DGO$. Иймээс $OG=EB=\dfrac{AB}{2}\Rightarrow AB=2OG$. Үүнтэй төстэйгээр $BC=2OH$, $CD=2OE$, $DA=2OF$. Эдгээрийг нэмбэл $$2(OE+OF+OG+OH)=AB+BC+CD+DA$$ болно.
2. $(2020+56\sqrt{1301})^m=(56+2020\sqrt{1301})^n$ байх $m$, $n$ натурал тоонууд олдохгүй гэдгийг батал.
Заавар Бодолт
Заавар.
Бодолт. Хэрэв
$$(2020+56\sqrt{1301})^m=(56+2020\sqrt{1301})^n$$
бол
$$(2020-56\sqrt{1301})^m=(56-2020\sqrt{1301})^n$$
биелэнэ. Гэтэл энэ тэнцэлийн зүүн гар талын модуль нь $1$-ээс бага, баруун гар талын модуль нь $1$-ээс их юм.
3. $56(x^2+y^2+z^2)+(77-x-2y+4z)^2\ge 4312$ тэнцэтгэл бишийг батал.
Заавар Бодолт
Заавар.
Бодолт. $77-x-2y+4z=t$ байх үед $56(x^2+y^2+z^2)+(77-x-2y+4z)^2$ илэрхийллийн хамгийн бага утгыг олъё. $(0,0,0)$ цэгээс
$$-x-2y+4z+77-t=0$$
хавтгай хүртэлх зай
$$d(t)=\dfrac{|77-t|}{\sqrt{(-1)^2+(-2)^2+4^2}}=\dfrac{|77-t|}{\sqrt{21}}$$
нөгөө талаас координатын эхээс $77-x-2y+4z=t$ байх аливаа $(x,y,z)$ цэг хүртэлх зай $\sqrt{x^2+y^2+z^2}$ нь $d(t)$-ээс багагүй байх нь ойлгомтой. Иймд
$$x^2+y^2+z^2\ge\dfrac{(77-t)^2}{21}$$
байна. Иймд
$$56(x^2+y^2+z^2)+(77-x-2y+4z)^2\ge\dfrac{56}{21}(77-t)^2+t^2$$
баруун гар талаас уламжлал авч минимум цэгийг нь олбол
$$\dfrac{112}{21}(t-77)+2t=0\Rightarrow t=56$$
болно. Иймд
$$56(x^2+y^2+z^2)+(77-x-2y+4z)^2\ge\dfrac{56}{21}(77-56)^2+56^2$$
буюу
$$56(x^2+y^2+z^2)+(77-x-2y+4z)^2\ge 56\cdot 77=4312$$
болж батлагдав. Координатын эхийг шүргэлтийн цэгтэй холбоход $77-x-2y+4z=t$ хавтгайн нормал гарч байх ёстой тул шүргэлтийн цэг нь $(-s,-2s,4s)$ координаттай байх ба $t=56$ үед
$$77+s+4s+16s=56\Rightarrow s=-1$$
буюу $(x,y,z)=(1,2,-4)$ үед тэнцэтгэл биш тэнцэлдээ хүрнэ.
4. $u_1=v_1=1$ ба
$$\left\{\begin{array}{l}u_{n+1}=3u_n+v_n\\ v_{n+1}=2u_n+4v_n\end{array}\right., n\in\mathbb N$$
гэж тодорхойлогдсон $u_n$, $v_n$ дарааллуудын ерөнхий гишүүний томьёог ол.
Заавар Бодолт
Заавар.
Бодолт. $A=\begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}$ гэвэл
$$\begin{pmatrix} u_{n+1}\\ v_{n+1}\end{pmatrix}=A\begin{pmatrix}u_{n}\\ v_{n}\end{pmatrix}$$
тул
$$\begin{pmatrix} u_{n}\\ v_{n}\end{pmatrix}=A^{n-1}\begin{pmatrix} u_{1}\\ v_{1}\end{pmatrix}\qquad (*)$$
байна.
$A$ матрицын хувийн утгууд нь $$\begin{vmatrix} 3-x & 1\\ 2 & 4-x\end{vmatrix}=0\Rightarrow (3-x)(4-x)-2=0\Rightarrow x_1=2, x_2=5$$ ба харгалзах хувийн векторууд нь $\begin{pmatrix} \hfill 1\\ -1\end{pmatrix}$, $\begin{pmatrix} 1\\ 2\end{pmatrix}$ буюу $$\begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}\begin{pmatrix} \hfill 1\\ -1\end{pmatrix}=2\begin{pmatrix} \hfill 1\\ -1\end{pmatrix},\quad \begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}\begin{pmatrix} 1\\ 2\end{pmatrix}=5\begin{pmatrix} 1\\ 2\end{pmatrix}$$ тул $$\begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}=\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}\begin{pmatrix} 2 & 0\\ 0 & 5\end{pmatrix}$$ болно. Эндээс $$\begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}=\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}\begin{pmatrix} 2 & 0\\ 0 & 5\end{pmatrix}\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}^{-1}$$ ба $$\begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}^{n-1}=\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}\begin{pmatrix} 2 & 0\\ 0 & 5\end{pmatrix}^{n-1}\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}^{-1}$$ болно. Иймд $$\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}^{-1}=\dfrac{1}{3}\begin{pmatrix} 2 & -1\\ 1 & \hfill 1\end{pmatrix}$$ болохыг тооцвол \begin{align*} \begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}^{n-1}&=\dfrac{1}{3}\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}\begin{pmatrix} 2^{n-1} & 0\\ 0 & 5^{n-1}\end{pmatrix}\begin{pmatrix} 2 & -1\\ 1 & \hfill 1\end{pmatrix}\\ &=\dfrac13\begin{pmatrix} 2^{n-1} & 5^{n-1}\\ -2^{n-1} & 2\cdot 5^{n-1}\end{pmatrix}\begin{pmatrix} 2 & -1\\ 1 & \hfill 1\end{pmatrix}\\ &=\dfrac13\begin{pmatrix} 2^{n}+5^{n-1} & -2^{n-1}+5^{n-1}\\ -2^{n}+2\cdot 5^{n-1} & 2^{n-1}+2\cdot 5^{n-1}\end{pmatrix} \end{align*} болно. Иймд $(*)$-оос $$u_n=\dfrac{2^{n-1}+2\cdot 5^{n-1}}{3},$$ $$v_n=\dfrac{-2^{n-1}+4\cdot 5^{n-1}}{3}$$ болно.
$A$ матрицын хувийн утгууд нь $$\begin{vmatrix} 3-x & 1\\ 2 & 4-x\end{vmatrix}=0\Rightarrow (3-x)(4-x)-2=0\Rightarrow x_1=2, x_2=5$$ ба харгалзах хувийн векторууд нь $\begin{pmatrix} \hfill 1\\ -1\end{pmatrix}$, $\begin{pmatrix} 1\\ 2\end{pmatrix}$ буюу $$\begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}\begin{pmatrix} \hfill 1\\ -1\end{pmatrix}=2\begin{pmatrix} \hfill 1\\ -1\end{pmatrix},\quad \begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}\begin{pmatrix} 1\\ 2\end{pmatrix}=5\begin{pmatrix} 1\\ 2\end{pmatrix}$$ тул $$\begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}=\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}\begin{pmatrix} 2 & 0\\ 0 & 5\end{pmatrix}$$ болно. Эндээс $$\begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}=\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}\begin{pmatrix} 2 & 0\\ 0 & 5\end{pmatrix}\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}^{-1}$$ ба $$\begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}^{n-1}=\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}\begin{pmatrix} 2 & 0\\ 0 & 5\end{pmatrix}^{n-1}\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}^{-1}$$ болно. Иймд $$\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}^{-1}=\dfrac{1}{3}\begin{pmatrix} 2 & -1\\ 1 & \hfill 1\end{pmatrix}$$ болохыг тооцвол \begin{align*} \begin{pmatrix} 3 & 1\\ 2 & 4\end{pmatrix}^{n-1}&=\dfrac{1}{3}\begin{pmatrix} \hfill 1 & 1\\ -1 & 2\end{pmatrix}\begin{pmatrix} 2^{n-1} & 0\\ 0 & 5^{n-1}\end{pmatrix}\begin{pmatrix} 2 & -1\\ 1 & \hfill 1\end{pmatrix}\\ &=\dfrac13\begin{pmatrix} 2^{n-1} & 5^{n-1}\\ -2^{n-1} & 2\cdot 5^{n-1}\end{pmatrix}\begin{pmatrix} 2 & -1\\ 1 & \hfill 1\end{pmatrix}\\ &=\dfrac13\begin{pmatrix} 2^{n}+5^{n-1} & -2^{n-1}+5^{n-1}\\ -2^{n}+2\cdot 5^{n-1} & 2^{n-1}+2\cdot 5^{n-1}\end{pmatrix} \end{align*} болно. Иймд $(*)$-оос $$u_n=\dfrac{2^{n-1}+2\cdot 5^{n-1}}{3},$$ $$v_n=\dfrac{-2^{n-1}+4\cdot 5^{n-1}}{3}$$ болно.