Бүс, дүүрэг 2019, намар,Бага ангийн багш
Бодлогын тоо: 4 Хугацаа: 150 мин
1.Ямар нэг $n$ натурал тооны хувьд $m=n-S(n)$ гэж бичигдэх $m$ натурал тоог "сайн тоо" гэж нэрлэе. 2019-өөс хэтрэхгүй хэчнээн ширхэг сайн тоо байх вэ? Энд $S(n)$ нь $n$ тооны цифрүүдийн нийлбэр.
Заавар Бодолт
Заавар.
Бодолт.Хариу: 202 ширхэг тоо.
5 буюу түүнээс дээш оронтой тооноос цифрүүдийнх нь нийлбэрийг хасахад $2019$-ээс их тоо гарах нь ойлгомжтой юм. Иймд зөвхөн 4 ба түүнээс цөөн оронтой тоонуудыг авч үзэхэд хангалттай. $m=n-S(n)$ ба $n=\overline{abcd}$ гэвэл $m=999a+99b+9c$ болно. Энд $a\in\{0,1,2\}$ ба $b,c\in\{0,1,2,\dots,9\}$ байна. $$m=999a+99b+c=999a^\prime+99b^\prime+9c^\prime$$ бол $a=a^\prime$, $b=b^\prime$, $c=c^\prime$ байх нь ойлгомжтой. $a=0\lor 1$ үед $b$, $c$ нь тус бүр 10 боломжтой ба үүнээс $a=b=c=0$ үед натурал тоо үүсэхгүй тул нийт $2\cdot 10\cdot 10-1=199$ ширхэг сайн тоо байна. Харин $a=2$ үед $m\le 2019$ байхын тулд $b=0$, $c=0,1,2$ байх тул 3 ширхэг сайн тоо байна. Иймд нийт 202 ширхэг сайн тоо байна.
5 буюу түүнээс дээш оронтой тооноос цифрүүдийнх нь нийлбэрийг хасахад $2019$-ээс их тоо гарах нь ойлгомжтой юм. Иймд зөвхөн 4 ба түүнээс цөөн оронтой тоонуудыг авч үзэхэд хангалттай. $m=n-S(n)$ ба $n=\overline{abcd}$ гэвэл $m=999a+99b+9c$ болно. Энд $a\in\{0,1,2\}$ ба $b,c\in\{0,1,2,\dots,9\}$ байна. $$m=999a+99b+c=999a^\prime+99b^\prime+9c^\prime$$ бол $a=a^\prime$, $b=b^\prime$, $c=c^\prime$ байх нь ойлгомжтой. $a=0\lor 1$ үед $b$, $c$ нь тус бүр 10 боломжтой ба үүнээс $a=b=c=0$ үед натурал тоо үүсэхгүй тул нийт $2\cdot 10\cdot 10-1=199$ ширхэг сайн тоо байна. Харин $a=2$ үед $m\le 2019$ байхын тулд $b=0$, $c=0,1,2$ байх тул 3 ширхэг сайн тоо байна. Иймд нийт 202 ширхэг сайн тоо байна.
2.Аль ч хоёрынх нь нийлбэр ялгавартаа хуваагддаг, $2019$ ширхэг натурал тоо оршин байх уу?
Заавар Бодолт
Заавар.
Бодолт.Ийм тоонуудыг индукцээр байгуулж болно. $a_1 < a_2 < \dots < a_n$ тоонууд бодлогын нөхцөлийг хангах тоонууд байг.
$$N=\prod_{i=1}^n a_i \prod_{i < j}(a_j-a_i)$$
гэвэл
$$N, a_1+N, a_2+N,\dots, a_n+N$$
тоонууд бодлогын нөхцөлийг хангана. Учир нь $a_i\mid N$ тул $N$, $a_i+N$ тоонуудын хувьд $a_i\mid a_j+2N$; $a_j-a_i\mid a_i+a_j$, $a_j-a_i\mid N$ тул $a_i+N$, $a_j+N$ тоонуудын хувьд $a_j-a_i\mid a_i+a_j+2N$ юм.
3.$a$ талтай $ABCD$ квадратын $AB$ тал дээр $P$ цэгийг, $BC$ тал дээр $Q$ цэгийг, $CD$ тал дээр $R$ цэгийг, $AD$ тал дээр $S$ цэгийг тус тус авав. Хэрэв $AP+AS+CQ+CR=2a$ байсан бол $PR=QS$ гэж батал.
Заавар Бодолт
Заавар.
Бодолт.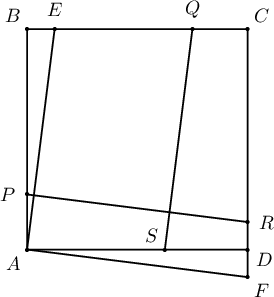
$A$-г дайрсан $QS$-тэй параллел шулуун $BC$ шулуунтай $E$ цэгт, $A$-г дайрсан $PR$-тай параллел шулуун $CD$ шулуунтай $F$ цэгт огтлолцдог байг. Тэгвэл $AS=EQ$, $AP=RF$ учраас $AP+AS+CQ+CR=EC+CF=2a$ буюу $EC=2a-CF$ болно. $BE=a-EC=a-(2a-CF)=CF-a=CF-CD=DF$, $AB=AD$, $\angle ABE=\angle ADF=90^{\circ}$ учраас $\triangle ABE= \triangle ADF$ болох ба $AE=AF$ байна. Эндээс $SQ=PR$ байна.
4.$5\times 5$ хүснэгтийн нүд бүрд натурал тоо бичжээ. Хүснэгтийн мөрнүүдэд бичсэн тоонуудын нийлбэр $S_1,S_2,S_3,S_4,S_5$, багануудад бичигдсэн тоонуудын нийлбэр $S_6, S_7, S_8, S_9, S_{10}$ болог. Хэрэв эдгээр 10 тоо бүгд ялгаатай байвал ийм хүснэгтийг "шидэт биш квадрат" гэе. Шидэт биш квадратад бичигдсэн бүх тоонуудын нийлбэр хамгийн багадаа хэд байж болох вэ?
Заавар Бодолт
Заавар.
Бодолт.Хариу: 48.
$S_1, S_2,\dots, S_{10}\ge 5$ байх нь ойлгомжтой. Эдгээр тоонууд бүгд ялгаатай гэдгээс $\{S_1,S_2,\dots,S_{10}\}$ олонлогийн байж болох "хамгийн бага" хувилбар нь $\{5,6,\dots,13,14\}$ юм. ($S_1+S_2+\dots+S_{10}$ нийлбэрийн хамгийн бага утгатай байх хувилбар). Хүснэгтэд бичигдсэн бүх тоонуудын нийлбэрийг $S$ гэе. Тэгвэл $$S=\dfrac12\cdot(S_1+S_2+\dots+S_{10})\ge\dfrac12(5+6+\dots+14)=\dfrac12\cdot 95=47\dfrac12$$ болж $S\ge 48$ болно. Одоо $S=48$ байх жишээ дурдахад хангалттай. Тухайлбал
$S_1, S_2,\dots, S_{10}\ge 5$ байх нь ойлгомжтой. Эдгээр тоонууд бүгд ялгаатай гэдгээс $\{S_1,S_2,\dots,S_{10}\}$ олонлогийн байж болох "хамгийн бага" хувилбар нь $\{5,6,\dots,13,14\}$ юм. ($S_1+S_2+\dots+S_{10}$ нийлбэрийн хамгийн бага утгатай байх хувилбар). Хүснэгтэд бичигдсэн бүх тоонуудын нийлбэрийг $S$ гэе. Тэгвэл $$S=\dfrac12\cdot(S_1+S_2+\dots+S_{10})\ge\dfrac12(5+6+\dots+14)=\dfrac12\cdot 95=47\dfrac12$$ болж $S\ge 48$ болно. Одоо $S=48$ байх жишээ дурдахад хангалттай. Тухайлбал
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 2 | 2 |
| 1 | 1 | 2 | 3 | 3 |
| 1 | 2 | 2 | 3 | 3 |
| 2 | 3 | 3 | 3 | 4 |