Бүс, дүүрэг 2019, намар,10-р анги
Бодлогын тоо: 4 Хугацаа: 180 мин
1.$a^3+b^3+c^3=3$ байх $a$, $b$, $c$ эерэг бодит тоонуудын хувьд
$$\dfrac{1}{a^4+3}+\dfrac{1}{b^4+3}+\dfrac{1}{c^4+3}\ge\dfrac{3}{4}$$
тэнцэтгэл биш биелэхийг батал.
Заавар Бодолт
Заавар.
Бодолт.$$\dfrac{1}{a^4+3}+\dfrac{1}{b^4+3}+\dfrac{1}{c^4+3}=\dfrac13\left(3-\dfrac{a^4}{a^4+3}-\dfrac{b^4}{b^4+3}-\dfrac{c^4}{c^4+3}\right)\ge\dfrac34$$
$$\Leftrightarrow\dfrac{a^4}{a^4+3}+\dfrac{b^4}{b^4+3}+\dfrac{c^4}{c^4+3}\le\dfrac34$$
болохыг батлахад хангалттай.
$a>0$ бол $\dfrac{a^4}{a^4+3}\le\dfrac{a^3}{4}$ гэдгийг баталъя. Энэ нь $4a\le a^4+3$ гэсэн илэрхий тэнцэтгэл биштэй эквивалент юм. ($a^4+3=a^4+1+1+1\ge4\sqrt[4]{a^4\cdot 1\cdot 1\cdot 1}=4a$)
Эндээс $$\dfrac{a^4}{a^4+3}+\dfrac{b^4}{b^4+3}+\dfrac{c^4}{c^4+3}\le\dfrac{a^3+b^3+c^2}{4}=\dfrac{3}{4}$$ болж бодлого бодогдоно. Баталгааны явцаас өгөгдсөн тэнцэтгэл бишийн тэнцэлдээ хүрэх нөхцөл $a=b=c=1$ болно.
$a>0$ бол $\dfrac{a^4}{a^4+3}\le\dfrac{a^3}{4}$ гэдгийг баталъя. Энэ нь $4a\le a^4+3$ гэсэн илэрхий тэнцэтгэл биштэй эквивалент юм. ($a^4+3=a^4+1+1+1\ge4\sqrt[4]{a^4\cdot 1\cdot 1\cdot 1}=4a$)
Эндээс $$\dfrac{a^4}{a^4+3}+\dfrac{b^4}{b^4+3}+\dfrac{c^4}{c^4+3}\le\dfrac{a^3+b^3+c^2}{4}=\dfrac{3}{4}$$ болж бодлого бодогдоно. Баталгааны явцаас өгөгдсөн тэнцэтгэл бишийн тэнцэлдээ хүрэх нөхцөл $a=b=c=1$ болно.
2.$ABCD$ параллелограммын $AB$ тал дээр $E$ цэгийг $AE:EB=1:3$ байхаар, $BC$ тал дээр $F$ цэгийг $BF:FC=3:2$ байхаар, $AD$ тал дээр $G$ цэгийг $AG:GD=1:4$ байхаар тус тус авав. Тэгвэл $EC$, $GF$, $BD$ шулуунууд нэг цэгт огтлолцохыг батал.
Заавар Бодолт
Заавар.
Бодолт.$EC\cap BD=O$ гэе.
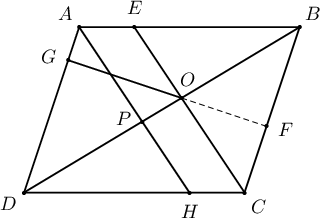$A$-г дайруулан $EC$-тэй параллел шулуун татъя. Энэ шулуун $BD$-тэй $P$ цэгт, $CD$-тэй $H$ цэгт огтлолцдог байг. Тэгвэл
$$\dfrac{OP}{OB}=\dfrac{AE}{EB}=\dfrac{1}{3}$$
байна. Хэрэв $OP=x$ гэвэл $OB=3x$ байна. $AECH$ параллелограмм учир $AE=CH$. Иймд $DH=EB$, $\measuredangle PHD=\measuredangle OEB$, $\measuredangle PDH=\measuredangle EBO$ учир $\triangle DPH=\triangle BOE$. Иймд $DP=OB=3x$. Хэрэв $AG=y$ гэвэл $DG=4y$ тул $BC=AD=5y$ байна. Иймд $BF=3y$, $FC=2y$ болно.
$$\dfrac{DG}{BF}=\dfrac{4y}{3y}=\dfrac{4}{3},\quad \dfrac{DO}{OB}=\dfrac{DP+OP}{OB}=\dfrac{3x+x}{3x}=\dfrac{4}{3}$$
$\measuredangle GDO=\measuredangle OBF\Rightarrow \triangle DGO\sim\triangle BFO\Rightarrow\measuredangle GOD=\measuredangle BOF$ учраас $G$, $O$, $P$ цэгүүд нэг шулуун дээр оршино.
3.$5\times 5$ хүснэгтийн нүд бүрд натурал тоо бичжээ. Хүснэгтийн мөрнүүдэд бичсэн тоонуудын нийлбэр $S_1,S_2,S_3,S_4,S_5$, багануудад бичигдсэн тоонуудын нийлбэр $S_6, S_7, S_8, S_9, S_{10}$ болог. Хэрэв эдгээр 10 тоо бүгд ялгаатай байвал ийм хүснэгтийг "шидэт биш квадрат" гэе. Шидэт биш квадратад бичигдсэн бүх тоонуудын нийлбэр хамгийн багадаа хэд байж болох вэ?
Заавар Бодолт
Заавар.
Бодолт.Хариу: 48.
$S_1, S_2,\dots, S_{10}\ge 5$ байх нь ойлгомжтой. Эдгээр тоонууд бүгд ялгаатай гэдгээс $\{S_1,S_2,\dots,S_{10}\}$ олонлогийн байж болох "хамгийн бага" хувилбар нь $\{5,6,\dots,13,14\}$ юм. ($S_1+S_2+\dots+S_{10}$ нийлбэрийн хамгийн бага утгатай байх хувилбар). Хүснэгтэд бичигдсэн бүх тоонуудын нийлбэрийг $S$ гэе. Тэгвэл $$S=\dfrac12\cdot(S_1+S_2+\dots+S_{10})\ge\dfrac12(5+6+\dots+14)=\dfrac12\cdot 95=47\dfrac12$$ болж $S\ge 48$ болно. Одоо $S=48$ байх жишээ дурдахад хангалттай. Тухайлбал
$S_1, S_2,\dots, S_{10}\ge 5$ байх нь ойлгомжтой. Эдгээр тоонууд бүгд ялгаатай гэдгээс $\{S_1,S_2,\dots,S_{10}\}$ олонлогийн байж болох "хамгийн бага" хувилбар нь $\{5,6,\dots,13,14\}$ юм. ($S_1+S_2+\dots+S_{10}$ нийлбэрийн хамгийн бага утгатай байх хувилбар). Хүснэгтэд бичигдсэн бүх тоонуудын нийлбэрийг $S$ гэе. Тэгвэл $$S=\dfrac12\cdot(S_1+S_2+\dots+S_{10})\ge\dfrac12(5+6+\dots+14)=\dfrac12\cdot 95=47\dfrac12$$ болж $S\ge 48$ болно. Одоо $S=48$ байх жишээ дурдахад хангалттай. Тухайлбал
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 2 | 2 |
| 1 | 1 | 2 | 3 | 3 |
| 1 | 2 | 2 | 3 | 3 |
| 2 | 3 | 3 | 3 | 4 |
4.$f(x)=x^5+x^4+1$ байг. Ямар нэг натурал тоо $n$-ийн хувьд $f(n)$ нь яг 6 ялгаатай натурал тоон хуваагчтай бол $n^3-n+1$ нь натурал тооны квадрат болохыг батал.
Заавар Бодолт
Заавар.
Бодолт.$f(1)=3$, $f(2)=49$ тоонууд яг 6 ялгаатай натурал тоон хуваагчгүй. Иймд $n\ge 3$. Яг 6 ялгаатай натурал тоон хуваагчтай тоо нь $p^5$ эсвэл $p^2q$ (энд $p$, $q$ - ялгаатай анхны тоонууд) хэлбэртэй болохыг хялбархан харж болно. Түүнчлэн
$$n^5+n^4+1=(n^3-n+1)\cdot(n^2+n+1)$$
байна. $(n^3-n+1,n^2+n+1)=d$ гэе. Тэгвэл
$$d\mid (n-2)=(n-1)(n^2+n+1)-(n^3-n+1)$$
бөгөөд эндээс
$$d\mid (n^2+n+1)-(n+3)(n-2)=7$$
болж $d=1$ эсвэл $d=7$ байна.
а) $d=1$ байг.
Энэ тохиолдолд $f(n)$-ийн нэг үржигдэхүүн $p^2$-тай нөгөө нь $q$-тэй тэнцүү байх ба $$n^2
б) $d=7$ байг.
Энэ тохиолдолд $7^2\mid f(n)$ болж $f(n)=7^2q$ эсвэл $f(n)=7^5$ болно. (энд $q\neq 7$ анхын тоо!)
(б1) $f(n)=7^2q$ байвал түүний үржигдэхүүнд $7$ ба $7q$ байхаас аргагүй.
(б2) $f(n)=7^5$ байвал түүний үржигдэхүүнд $7$ ба $7^4$ болж аль ч тохиолдолд $(n^2+n+1)$ ба $n^3-n+1$ үржигдэхүүнүүдийн аль нэг нь $7$-той тэнцүү болно. Гэвч $n\ge 3$ үед ийм байх боломжгүй.
а) $d=1$ байг.
Энэ тохиолдолд $f(n)$-ийн нэг үржигдэхүүн $p^2$-тай нөгөө нь $q$-тэй тэнцүү байх ба $$n^2
б) $d=7$ байг.
Энэ тохиолдолд $7^2\mid f(n)$ болж $f(n)=7^2q$ эсвэл $f(n)=7^5$ болно. (энд $q\neq 7$ анхын тоо!)
(б1) $f(n)=7^2q$ байвал түүний үржигдэхүүнд $7$ ба $7q$ байхаас аргагүй.
(б2) $f(n)=7^5$ байвал түүний үржигдэхүүнд $7$ ба $7^4$ болж аль ч тохиолдолд $(n^2+n+1)$ ба $n^3-n+1$ үржигдэхүүнүүдийн аль нэг нь $7$-той тэнцүү болно. Гэвч $n\ge 3$ үед ийм байх боломжгүй.