Бүс, дүүрэг 2019, намар Монгол Бодлогын Сан

Бүс, дүүрэг 2019, намар, 9-р анги

Бүс, дүүрэг 2019, 9-р анги

Бодлогын тоо: 4 Хугацаа: 180 мин

$n$ натурал тоо бол

$2^n+3^n$ тоо бүхэл тооны квадрат болох уу?

Заавар Бодолт

Заавар.

Бодолт. Тэгш

$n$ -ийн хувьд сүүлийн цифр нь 3 юмуу 7 байна. Харин сондгой

$n$ -ийн хувьд 3-д хуваахад 2 үлдэгдэгдэл өгнө.

$n=x+y+(x,y)+[x,y]$ байхаар

$x$ ,

$y$ натурал тоо олддог бол

$n$ натурал тоог "сайн тоо" гэе. Эхний 2019 натурал тоон дотор хэдэн "сайн тоо" байгаа вэ? Энд

$(x,y)$ -ээр

$x$ ,

$y$ тоонуудын ХИЕХ-г,

$[x,y]$ -ээр

$x$ ,

$y$ тоонуудын ХБЕХ-г тэмдэглэв.

Заавар Бодолт

Заавар.

Бодолт. Хариу:

$1008$ сайн тоо бий.

Ерөнхий тохиолдолд

$n>2$ , тэгш тоо бүр "сайн тоо" бөгөөд аливаа сондгой тоо сайн тоо болохгүй гэдгийг баталъя. Хэрэв

$x$ ба

$y$ нь тэгш сондгойгоороо ижил тоонууд байвал

$x$ ,

$y$ ,

$(x,y)$ ,

$[x,y]$ тоонууд тэгш сондгойгоорой ижилхэн тоонууд байх тул тэдгээрийн нийлбэр тэгш тоо байна. Хэрэв

$x$ ,

$y$ нь тэгш сондгойгоорой өөр, өөр тоонууд байвал

$(x,y)$ сондгой тоо,

$[x,y]$ тэгш тоо тул

$x$ ,

$y$ ,

$(x,y)$ ,

$[x,y]$ гэсэн 4 тооны яг 2 нь тэгш 2 нь сондгой тоо байна. Иймд эдгээрийн нийлбэр тэгш тоо. Түүнчлэн

$x$ ,

$y\ge 1$ гэдгээс

$n\ge 4$ байх нь ойлгомжтой. Нөгөө талаас

$n$ нь

$2$ -оос их дурын тэгш тоо бол

$x=1$ ,

$y=\dfrac{n}{2}-1$ гэж сонговол

$(x,y)=1$ ба

$[x,y]=y=\dfrac{n}{2}-1$ тул

$x+y+(x,y)+[x,y]=n$ болж

$2$ -оос их тэгш тоо бүр "сайн тоо" болов.

3. Өгөгдсөн 2000 бүхэл тоог дурын байдлаар 1000 хосд хуваагаад хос бүрийн тоонуудын нийлбэрийг бодоход нийлбэрүүд дунд хоорондоо тэнцүү хоёр тоо ямагт олдож байв. Тэгвэл эдгээр тоон дотор хамгийн олондоо хэдэн ялгаатай тоо байж болох вэ?

Заавар Бодолт

Заавар.

Бодолт. Хариу: 999 тоо.

Хэрэв эдгээр 2000 тоон дотор хоорондоо ялгаатай 1000 тоо байдаг гэвэл тэдгээрийг

$a_1 < a_2 < \dots < a_{1000}$ гэж эрэмбэлсэн гэе. Үлдсэн 1000 тоог мөн

$b_1 \le b_2 \le \dots \le b_{1000}$ гэж эрэмбэлье. Дараа нь

$(a_1,b_1), (a_2,b_2),\dots,(a_{1000}, b_{1000})$ гэж 1000 хос үүсгэе. Тэгвэл

$a_1+b_1 < a_2+b_2 < \dots < a_{1000}+b_{100}$ болоход хүрч зөрчилд хүрнэ. Иймд эдгээр 2000 тоон дотор 1000-аас цөөн тооны ялгаатай тоонууд байна. Харилцан ялгаатай тоонууд нийт 999 байж болох жишээ нь

$\underbrace{1,1,\ldots,1}_{1002},2,3,4,\dots,998,999$ гэсэн 2000 тоо юм.

$ABCD$ параллелограммын

$AB$ тал дээр

$E$ цэгийг

$AE:EB=1:3$ байхаар,

$BC$ тал дээр

$F$ цэгийг

$BF:FC=3:2$ байхаар,

$AD$ тал дээр

$G$ цэгийг

$AG:GD=1:4$ байхаар тус тус авав. Тэгвэл

$EC$ ,

$GF$ ,

$BD$ шулуунууд нэг цэгт огтлолцохыг батал.

Заавар Бодолт

Заавар.

Бодолт.

$EC\cap BD=O$ гэе.

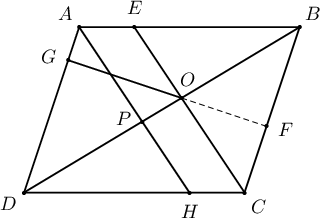$A$ -г дайруулан

$EC$ -тэй параллел шулуун татъя. Энэ шулуун

$BD$ -тэй

$P$ цэгт,

$CD$ -тэй

$H$ цэгт огтлолцдог байг. Тэгвэл

$\dfrac{OP}{OB}=\dfrac{AE}{EB}=\dfrac{1}{3}$ байна. Хэрэв

$OP=x$ гэвэл

$OB=3x$ байна.

$AECH$ параллелограмм учир

$AE=CH$ . Иймд

$DH=EB$ ,

$\measuredangle PHD=\measuredangle OEB$ ,

$\measuredangle PDH=\measuredangle EBO$ учир

$\triangle DPH=\triangle BOE$ . Иймд

$DP=OB=3x$ . Хэрэв

$AG=y$ гэвэл

$DG=4y$ тул

$BC=AD=5y$ байна. Иймд

$BF=3y$ ,

$FC=2y$ болно.

$\dfrac{DG}{BF}=\dfrac{4y}{3y}=\dfrac{4}{3},\quad \dfrac{DO}{OB}=\dfrac{DP+OP}{OB}=\dfrac{3x+x}{3x}=\dfrac{4}{3}$

$\measuredangle GDO=\measuredangle OBF\Rightarrow \triangle DGO\sim\triangle BFO\Rightarrow\measuredangle GOD=\measuredangle BOF$ учраас

$G$ ,

$O$ ,

$P$ цэгүүд нэг шулуун дээр оршино.

Бүс, дүүрэг 2019, намар, 9-р анги

Санал хүсэлт: