Заавар.

Бодолт. $\displaystyle A=B\sum\limits_{n\in S_{m}}\dfrac{1}{n}=Bm\sum\limits_{(n\in S_{m},~n<\frac{m}{2})} \left(\dfrac{1}{n}\cdot\dfrac{1}{m-n}\right)$ ба $(m,6)=1$ тул $$6\cdot\kern-13pt\sum\limits_{n\in S_{m}, n < m/2}\kern-13pt n^{-1}\cdot (m-n)^{-1}\equiv 3\cdot\sum\limits_{n\in S_{m}} n^{-1}(m-n)^{-1}\equiv 0\pmod{m}$$ гэж батлахад хангалттай. $(m-n)^{-1}\equiv -n^{-1}\pmod{m}$, $$S_{m}=\{n^{-1}\mid n\in S_{m}\}\pmod{m}=\{2n\mid n\in S_{m}\}\pmod{m}$$ гэдгийг тооцвол \begin{align*} 3\sum\limits_{1\in S_{m}}n^{-1}(m-n)^{-1}&\equiv -3\sum\limits_{n\in S_{m}}(n^{-1})^{2}\\ &\equiv -3\sum\limits_{n\in S_{m}}n^{2}\\ &\equiv\sum\limits_{n\in S_{m}}n^{2}-\sum\limits_{n\in S_{m}}(2n)^{2}\\ &\equiv 0\pmod{m} \end{align*} болж батлагдав.

Заавар.

Бодолт. $S$ олонлогийн ямар нэг $\pi$ сэлгэмлийг авъя. Хэрэв $\pi$ сэлгэмэлд $A_{i}$-ийн бүх элемент, $B_{i}$-ийн элементүүдийн өмнө ордог бол $\pi$-г $i$-р төрлийнх гэе. Одоо $\pi$ нь нэгэн зэрэг $i$ ба $j$-р төрлийнх байж болохгүйг баталъя. Эсрэгээс нь $\pi$ нь $i$ ба $j$-р төрлийнх байг. $x_{i}$ нь $A_{i}$-ийн $\pi$ дэх хамгийн сүүлчийн элемент, $x_{p}$ нь $A_{p}$-ийн $\pi$ дэх хамгийн сүүлчийн элементийг тус тус тэмдэглэж байг. Хэрэв $x_{i}$ нь $x_{j}$-ээс хойш байрладаггүй бол $A_{i}\cap B_{j}=\varnothing$ болох тул зөрчил үүснэ. Иймд $\pi$ нь зөвхөн нэг л төрлийнх байж болно. Одоо $i$-р төрлийн сэлгэмэлийн тоог олъё. Энэ нь $$C_{n}^{k+\ell}\cdot(n-k-\ell)!\cdot k!\cdot \ell!=\frac{n!}{C_{k+\ell}^{k}}$$ Эдгээрийг нэмэхэд батлах зүйл батлагдана.

Заавар.

Бодолт. Диагоналиудын огтлолцлын цэгийг $O$ гэе. $ANP$, $POQ$ 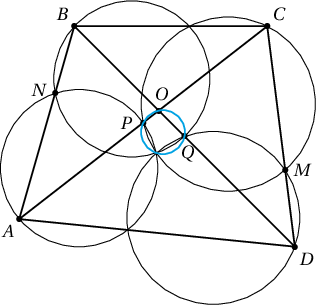гурвалжнуудыг багтаасан тойргууд $K$ цэгт огтлолцдог байг.

$\measuredangle OQP=\measuredangle OKP$, $\measuredangle BNP=\measuredangle AKP$ учир $$\measuredangle ABO=180^\circ -(\measuredangle BNP+\measuredangle OQP)=180^\circ-(\measuredangle AKP + \measuredangle OKP)=180^\circ-\measuredangle AKO$$ буюу $ABOK$ дөрвөн өнцөгт тойрогт багтана. Яг ижил аргаар $NBQK$ нэг тойрог дээр оршино. $\measuredangle BQK=180^\circ-\measuredangle OPK=\measuredangle APK$ ба $\measuredangle KBQ=\measuredangle OAK$ гэдгээс $$\triangle APK\sim\triangle BQK\Rightarrow\frac{AK}{BK}=\frac{BQ}{AP}=\frac{BD}{AC}$$ ба $\measuredangle DBK=\measuredangle CAK$ учир $\triangle ACK\sim\triangle BDK$ $\Rightarrow$ $\measuredangle OCK=\measuredangle ODK$ болж $OCDK$ дөрвөн өнцөгт тойрогт багтана. Эндээс $$\measuredangle KDC=\measuredangle POK=\measuredangle PQK=180^\circ -\measuredangle KQM$$ буюу $KQMD$ дөрвөн өнцөгт тойрогт багтана. Бас $\measuredangle KCM=\measuredangle KOD=\measuredangle KPQ$ буюу $PCMK$ дөрвөн өнцөгт тойрогт багтана. Үүгээр бодлого бодогдов.

Заавар.

Бодолт. $1,2,...,n-1,n+1$ тоонуудын, $\forall k$ $(1\leq k\leq n)$ тооны хувьд $|b_{k}-k|=0$, эсвэл 1, эсвэл 2 байх $b_{1},b_{2},...,b_{n}$ сэлгэмлийн тоог $B_{n}$ гэе. Тэгвэл $a_{n}=n$ байх сэлгэмлийн тоо $A_{n-1}$. $a_{n-1}=n$ байх сэлгэмлийн тоо нь $B_{n-1}=A_{n-2}+B_{n-2}$, $a_{n-2}=n$ байх сэлгэмлийн тоо нь $B_{n-2}+A_{n-3}+A_{n-4}$ болохыг төвөггүй харж болно. Иймд $$\left\{\begin{aligned}{l} A_{n}&=A_{n-1}+A_{n-2}+A_{n-3}+A_{n-4}+2B_{n-2}\\ &=A_{n-1}+A_{n-2}+A_{n-3}+A_{n-4}+2(A_{n-3}+B_{n-3})\\ A_{n-1}&=A_{n-2}+A_{n-3}+A_{n-4}+A_{n-5}+2B_{n-3}\end{aligned}\right.$$ Эдгээрийг хасвал $A_{n}=2A_{n-1}+2A_{n-3}-A_{n-5}$ болж батлах зүйл батлагдав.

Заавар.

Бодолт. $ABC$ гурвалжныг багтаасан тойргийг $\omega$; $[BD)$, $[DC)$ цацрагууд ба $\omega$ тойргийг гадаад байдлаар шүргэсэн тойргийг $\omega_1$; $\omega_1$ тойргийг $[BD)$, $[DC)$ цацрагуудыг шүргэх цэгийг $P,Q$; $B$ өнцгийн биссектрисийн $AC$-тэй огтлолцох цэгийг $L$; $B$ өнцөгт харгалзах гадаад багтсан тойргийн төвийн $O_3$; $(BL)\cap(PQ)=T$ гэе.

$A,B,C,\omega_1$ тойргууд $\omega$ тойргийг шүргэнэ. Кезийн теорем хэрэглэвэл: $AB\cdot CQ+BC\cdot AQ=AC\cdot BP$ $\Leftrightarrow$ $c\cdot CQ+a\cdot (b+CQ)=b\cdot BP$. Гэвч $CQ=DQ-DC=DP-DC=(BP-BD)-DC$ учраас $$BP\cdot(c+a-b)+ab=(a+c)(BD+DC)\qquad(1) $$ $$\begin{array}{l} BD+DC=(BP-DP)+DC=BP-DQ+DC=BP-CQ=\\ =BP-(LQ-LC)=BP-LQ+LC=BP+\frac{ab}{a+c}-LQ\qquad(2)\end{array}$$ (1) ба (2)-оос $BP(c+a-b)+ab=ab+(a+c)\cdot(BP-LQ)$ $\Leftrightarrow$ $$\frac{LQ}{BP}=\frac b{a+c}\qquad(3)$$

$BDL$ гурвалжин ба $QP$ огтлогчийн хувьд Менелайн теорем хэрэглэвэл: $\frac{LT}{TB}\cdot\frac{BP}{PD}\cdot\frac{DQ}{QL}=1$ $\Rightarrow$ $$\frac{LT}{TB}=\frac{PD}{BP}\cdot\frac{QL}{DQ}\stackrel{PD=DQ}{=\!=\!=\!=\!=}\frac{QL}{BP}\qquad(4)$$ (3) ба (4)-өөс $\frac{LT}{TB}=\frac b{a+c}$ гэж гарах тул $T\equiv O_b$ яагаад?

$\omega_1$ тойргийн төвийг $O_1$, $B$ өнцөгт харгалзах гадаад багтсан тойргийн $AC$ талтай шүргэлцэх цэгийг $K$ гэвэл $\triangle DQO_1\sim\triangle O_bKQ$ $\Rightarrow$ $\frac{KO_b}{DQ}=\frac{KQ}{QO_1}$ $\Rightarrow$ $$KO_b\cdot QO_1=DQ\cdot KQ\qquad(5) $$ $AC$ талын дундаж цэгийг $M$ гэвэл $DP\|O_bM$ (батал!). Иймээс $$\begin{array}{l}KO_b^2=O_bM^2-MK^2=MQ^2-MK^2=\\ ~~~~~=(MQ+MK)\cdot(MQ-MK)=DQ\cdot KQ\end{array}\qquad(6)$$ (5) ба (6)-аас $KO_b\cdot QO_1=KO_b^2$ $\Leftrightarrow$ $QO_1=KO_b$ гэж гарч батлах зүйл батлагдав.

Заавар.

Бодолт. $g$ нь 41 модулиархи анхны язгуур байг. Тойрог дээрх тоонууд маань 41 модулиар геометр прогресс үүсгэх тул ноогдвор нь $q=g^{\alpha}$ гэе. Тэгвэл тоонууд маань тойрог дээр $1, g^{\alpha}, g^{2\alpha}$, $...,g^{39\alpha}$ дарааллаар байрлана. Нөгөө талаас эдгээр нь ялгаатай байхын тулд $0\leq i < j\leq 40$ байх дурын $i, j$ тоонуудын хувьд $i\alpha\equiv j\alpha (40)$ буюу $(\alpha, 40)=1$ байх шаардлагатай. $\varphi (40)=40(1-\frac{1}{2})(1-\frac{1}{5})=16$. Нөгөө талаас ноогдвор нь $g^{\alpha}, g^{-\alpha}$ байх 2 байрлал тэгш хэмтэй тул нийт $\frac{16}{2}=8$ ялгаатай байрлал бий.