ММО-39, 10-р анги
Бодлогын тоо: 6 Хугацаа: 540 мин
1. Тэмцээнд $n$ $(n\ge10)$ баг оролцож тойргоор тоглов. Тэмцээний дараа нэг ч тэнцээ гараагүй ба тэнцүү оноотой 4 баг байсан бол бие биеэ тойрч хожсон гурвалын хос дор хаяад 2 олдохыг батал.
Заавар Бодолт
Заавар.
Бодолт. $A$ хүн $B$-г хожсон бол $A\longrightarrow B$ гэж тэмдэглэе. Тэнцүү оноотой 4 хүнээр үүсэх дэд графад чиглэлт гурвалжин үүсгэхгүй ямар нэг гурвал олдоно. Энэ гурвалын үүсгэх дэд графын хувьд $A$ хүнээс 2 сум гарсан $B$ хүнд 2 сум ирсэн гэж үзэж болно. Одоо графаа сэргээж харвал энэ 3-аас бусад хүмүүс рүү $B$-ээс гарсан сумын тоо $A$-аас гарснаас 2-оор илүү байна. Энэ нь $A$, $B$ хүмүүс оролцсон чиглэлт гурвалжин 2 олдохыг үзүүлж байна.
2. $\forall k\in\mathbb N$ хувьд $a_{k+1}>a_k$ байх ба $a_ka_{k+1}+1$ ба $a_k+1$ нь бүтэн квадрат байх натурал тоон төгсгөлгүй дараалал олдохыг батал.
3. $ABC$ гурвалжны ортотөв нь $H$ ба багтаасан тойргийн төв нь $O$ болог. $CO$ шулуун дээр орших дурын
$E$ цэгийн хувьд $AH\cap BE=M$, $BH\cap AE=N$ бол $\measuredangle ACN=\measuredangle BCM$ гэж батал.
Заавар Бодолт
Заавар.
Бодолт. $CO\cap AB=Y$, $AN\cap CB=X$ ба $BM\cap AC=Z$ гэж тус тус тэмдэглэе.
$$(BB_1,N)=(AA_1,M)\qquad(1)$$
гэж батлахад хангалттай юм. Мөн $\triangle ABC$-ын өнцгүүдийг харгалзан $\alpha$, $\beta$, $\gamma$ гэж тус тус тэмдэглэе.
$$(AB,Y)=\frac{\sin2\beta}{\sin2\alpha}\qquad(*)$$ гэдгийг хялбар харж болно.
$CBB_1$ гурвалжин, $AN$ огтлогчийн хувьд Менелайн теорем бичвэл $(CB,X)(BB_1,N)(B_1C,A)=-1$.
Мөн $\triangle CAA_1$ ба $BM$ огтлогчийн хувьд Менелайн теоремийг бичвэл $(CA,Z)(AA_1,M)(A_1C,B)=-1$ болох ба эндээс (1) $\Leftrightarrow$ $(CB,X)(B_1C,A)=(CA,Z)(A_1C,B)$ $\Leftrightarrow$ $$(CB,X)(AC,Z)=(A_1C,B)(CB_1,A)\qquad(2)$$ Нөгөө талаас Чевийн теоремоор $(CB,X)(BA,Y)(AC,Z)=1$ $\Rightarrow$ $$(CB,X)(AC,Z)=(AB,Y)\qquad(3)$$ (2) ба (3)-аас $(A_1C,B)(CB_1,A)=(AB,Y)$-ийг батлахад хангалттай. $(A_1C,B)=\dfrac{\ctg\beta}{\ctg\beta+\ctg\gamma}$, $(CB_1,A)=\dfrac{\ctg\alpha+\ctg\gamma}{\ctg\gamma}$ ба $(*)$-ыг анхаарвал батлах зүйл илэрхий юм. Бодлого бодогдов.
$CBB_1$ гурвалжин, $AN$ огтлогчийн хувьд Менелайн теорем бичвэл $(CB,X)(BB_1,N)(B_1C,A)=-1$.
Мөн $\triangle CAA_1$ ба $BM$ огтлогчийн хувьд Менелайн теоремийг бичвэл $(CA,Z)(AA_1,M)(A_1C,B)=-1$ болох ба эндээс (1) $\Leftrightarrow$ $(CB,X)(B_1C,A)=(CA,Z)(A_1C,B)$ $\Leftrightarrow$ $$(CB,X)(AC,Z)=(A_1C,B)(CB_1,A)\qquad(2)$$ Нөгөө талаас Чевийн теоремоор $(CB,X)(BA,Y)(AC,Z)=1$ $\Rightarrow$ $$(CB,X)(AC,Z)=(AB,Y)\qquad(3)$$ (2) ба (3)-аас $(A_1C,B)(CB_1,A)=(AB,Y)$-ийг батлахад хангалттай. $(A_1C,B)=\dfrac{\ctg\beta}{\ctg\beta+\ctg\gamma}$, $(CB_1,A)=\dfrac{\ctg\alpha+\ctg\gamma}{\ctg\gamma}$ ба $(*)$-ыг анхаарвал батлах зүйл илэрхий юм. Бодлого бодогдов.
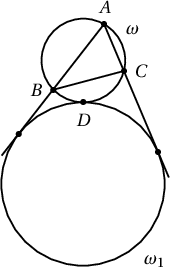
4. $\omega$ ба $\omega_1$ тойргууд нь $D$ цэгт шүргэлцэнэ. $AC$ ба $AB$ талууд $\omega_1$ тойргийг шүргэнэ.
$\measuredangle CDB$ өнцгийн биссектрисийг агуулсан шулуун $ABC$ гурвалжины ($CB$ талыг шүргэсэн) гадаад багтсан тойргийн төвийг дайрна гэж батал.

Заавар Бодолт
Заавар.
Бодолт. Эхлээд бодлого бодоход хэрэглэгдэх нэгэн леммийг томъёолон баталъя.
Архимедийн лемм. $\ell$ шулуун $\omega$ тойргийг $K$ ба $M$ цэгт огтолдог байг. $\omega$ тойргийг $P$ цэгт, $KM$ шулууныг $L$ цэгт шүргэх $\omega_1$ тойргийг авч үзье. $PL$ шулуун $\omega$ тойргийн $KM$ шулуунаар хуваагдсан хоёр нумын аль нэгнийх нь дундажийг дайрна.
Баталгаа. Зурагт дүрслэгдсэн шиг байрлалтай үед леммийг баталъя. Өөр байрлалтай тохиолдлуудад бие даан батлаарай. $\omega$ ба $\omega_1$ тойргийн $P$ цэгт татсан шүргэгч шулуун $KM$ шулуунтай огтлолцох цэгийг $Q$ гэе. $PL$ шулууны $\omega$ тойрогтой огтлолцох хоёр дахь цэгийг $E$ гэе. $PQ=LQ$ гэдгээс $$\measuredangle PLQ=\measuredangle QPL\qquad(1)$$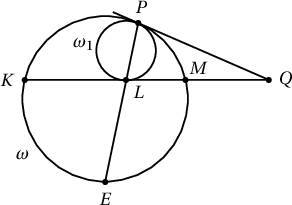 гэж гарна. Нөгөө талаас
$$\measuredangle PLQ=\measuredangle PLM=\dfrac12(\stackrel{\smile}{KE}+\stackrel{\smile}{PM})\qquad(2)$$
$$\measuredangle QPL=\measuredangle QPE=\dfrac12(\stackrel{\smile}{PM}+\stackrel{\smile}{ME})\qquad(3)$$
$(1)$, $(2)$, $(3)$-аас $\stackrel{\smile}{KE}=\stackrel{\smile}{ME}$ гэж гарна, ө.х.
$E$ нь $KEM$ нумын дундаж цэг. Лемм батлагдав.
гэж гарна. Нөгөө талаас
$$\measuredangle PLQ=\measuredangle PLM=\dfrac12(\stackrel{\smile}{KE}+\stackrel{\smile}{PM})\qquad(2)$$
$$\measuredangle QPL=\measuredangle QPE=\dfrac12(\stackrel{\smile}{PM}+\stackrel{\smile}{ME})\qquad(3)$$
$(1)$, $(2)$, $(3)$-аас $\stackrel{\smile}{KE}=\stackrel{\smile}{ME}$ гэж гарна, ө.х.
$E$ нь $KEM$ нумын дундаж цэг. Лемм батлагдав.
Одоо бодлогынхоо бодолтонд шилжье.
$AB$, $AC$ шулуунуудын $\omega_1$ тойргийг шүргэх цэгүүдийг харгалзан $P$, $Q$ гэж тэмдэглэе. $CDB$ өнцгийн биссектрисийг агуулсан шулууны $QP$ шулуунтай огтлолцсон цэгийг $F$ гэе. $QD$ шулууны $\omega$ тойрогтой огтлолцох хоёр дахь цэгийг $E$ гэе. Архимедийн лемм ёсоор $E$ нь $ABC$ нумын дундаж цэг болно.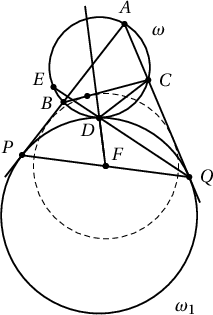 $F$ цэгийг $ABC$ гурвалжны $CB$ талыг шүргэсэн гадаад багтсан тойргийн төв болно гэж баталъя. Нэг талаас
$$\measuredangle CDF=\pi-\dfrac12\measuredangle BDC=\pi-\dfrac12(\pi-\alpha)=\dfrac{\pi}2+\dfrac{\alpha}2$$
Нөгөө талаас
$$\measuredangle CQF=\measuredangle AQP=\dfrac12(\pi-\measuredangle PAQ)=\dfrac{\pi}2-\dfrac{\alpha}{2}$$
тул
$$\measuredangle CDF+\measuredangle CQF=\pi$$
Иймд $DFQC$ дөрвөн өнцөгт тойрогт багтана.
Иймээс
\begin{align*}
\measuredangle QCF&=\measuredangle QDF=\measuredangle CDF-\measuredangle CDQ\\
&=\dfrac{\pi}2+\dfrac{\alpha}2-\measuredangle CDQ=\dfrac{\pi+\alpha}2-\dfrac14\stackrel{\smile}{ABC}\\
&=\dfrac{\pi+\alpha}2-\dfrac14(2\pi-2\beta)=\dfrac{\alpha+\beta}2
\end{align*}
болно. Ийнхүү $CF$ нь $BCQ$ өнцгийн биссектрис болно. Яг үүнтэй адилаар $BF$ нь $CBP$ өнцгийн биссектрис болно гэж батлагдана.
Бодлого бодогдов.
$F$ цэгийг $ABC$ гурвалжны $CB$ талыг шүргэсэн гадаад багтсан тойргийн төв болно гэж баталъя. Нэг талаас
$$\measuredangle CDF=\pi-\dfrac12\measuredangle BDC=\pi-\dfrac12(\pi-\alpha)=\dfrac{\pi}2+\dfrac{\alpha}2$$
Нөгөө талаас
$$\measuredangle CQF=\measuredangle AQP=\dfrac12(\pi-\measuredangle PAQ)=\dfrac{\pi}2-\dfrac{\alpha}{2}$$
тул
$$\measuredangle CDF+\measuredangle CQF=\pi$$
Иймд $DFQC$ дөрвөн өнцөгт тойрогт багтана.
Иймээс
\begin{align*}
\measuredangle QCF&=\measuredangle QDF=\measuredangle CDF-\measuredangle CDQ\\
&=\dfrac{\pi}2+\dfrac{\alpha}2-\measuredangle CDQ=\dfrac{\pi+\alpha}2-\dfrac14\stackrel{\smile}{ABC}\\
&=\dfrac{\pi+\alpha}2-\dfrac14(2\pi-2\beta)=\dfrac{\alpha+\beta}2
\end{align*}
болно. Ийнхүү $CF$ нь $BCQ$ өнцгийн биссектрис болно. Яг үүнтэй адилаар $BF$ нь $CBP$ өнцгийн биссектрис болно гэж батлагдана.
Бодлого бодогдов.
Архимедийн лемм. $\ell$ шулуун $\omega$ тойргийг $K$ ба $M$ цэгт огтолдог байг. $\omega$ тойргийг $P$ цэгт, $KM$ шулууныг $L$ цэгт шүргэх $\omega_1$ тойргийг авч үзье. $PL$ шулуун $\omega$ тойргийн $KM$ шулуунаар хуваагдсан хоёр нумын аль нэгнийх нь дундажийг дайрна.
Баталгаа. Зурагт дүрслэгдсэн шиг байрлалтай үед леммийг баталъя. Өөр байрлалтай тохиолдлуудад бие даан батлаарай. $\omega$ ба $\omega_1$ тойргийн $P$ цэгт татсан шүргэгч шулуун $KM$ шулуунтай огтлолцох цэгийг $Q$ гэе. $PL$ шулууны $\omega$ тойрогтой огтлолцох хоёр дахь цэгийг $E$ гэе. $PQ=LQ$ гэдгээс $$\measuredangle PLQ=\measuredangle QPL\qquad(1)$$

Одоо бодлогынхоо бодолтонд шилжье.
$AB$, $AC$ шулуунуудын $\omega_1$ тойргийг шүргэх цэгүүдийг харгалзан $P$, $Q$ гэж тэмдэглэе. $CDB$ өнцгийн биссектрисийг агуулсан шулууны $QP$ шулуунтай огтлолцсон цэгийг $F$ гэе. $QD$ шулууны $\omega$ тойрогтой огтлолцох хоёр дахь цэгийг $E$ гэе. Архимедийн лемм ёсоор $E$ нь $ABC$ нумын дундаж цэг болно.

5. $n$, $b$ нь өгөгдсөн натурал тоонууд, $\dfrac{a^n-b^n}{a-b}$ тоо нь ямар нэг тооны 1-ээс их зэрэг болдоггүй байхаар $(a,b)=1$ байх $a$ тоо төгсгөлгүй олон олдохыг батал.
Заавар Бодолт
Заавар.
Бодолт. Ямар нэг $p\in\mathbb P$ тооны хувьд
$$\left\{\begin{array}{ll}
\dfrac{a^n-b^n}{a-b}\equiv0\pmod{p} & (1)\\
\dfrac{a^n-b^n}{a-b}\not\equiv0\pmod{p^2}& (2)\\
(a,b)=1 & (3)
\end{array}\right.\qquad(*)
$$ байх $a\in\mathbb N$ төгсгөлгүй олон олдвол бодлого бодогдоно.
Арифметик прогресс дахь Дирихлейн теоремоор $p\equiv1\pmod{4n}$ байх хангалттай их анхны тоо $p$ олдоно. Тэгвэл $(b,p)=1$ гэж үзэж чадна.
$p=4nk+1$ байг. Модул $p$-ийн анхдагч язгуурыг $g\in\mathbb N$ гээд $$\left\{\begin{array}{l} a_1=g^{4k}b+p^2\ell\\ a_2=(p-g)^{4k}b+p^2\ell \end{array}\right.$$ гэе. $(\ell,b)=1$ бол $(a_1a_2,b)=1$ байна, ө.х. $a_1,a_2$ нь $(*)$-ын $(3)$-ыг хангав. Иймд $(\ell,b)=1$ бол $a_1,a_2$-ын аль нэг нь $(*)$-ын $(1)$ ба $(2)$-ыг хангана гэж харуулъя. $$a_1-b=(g^{4k}-1)b+p^2\ell\equiv(g^{4k}-1)b\not\equiv0\pmod{p},$$ $$a_1^n-b^n=(g^{4k}b+p^2\ell)^n-b^n\equiv(g^{4k}b)^n-b^n\equiv b^n(g^{4nk}-1)\equiv b^n(g^{p-1}-1)\equiv0\pmod{p}.$$ Эндээс $\dfrac{a_1^n-b^n}{a_1-b}\equiv0\pmod{p}$, ө.х. $(*)$-ын $(1)$ биелэв.
$p=4s+1$ хэлбэртэй тул МК-1, \S1.6 дасгал 11-ээр $p-g$ нь мөн модул $p$-ээр анхдагч язгуур учир $\dfrac{a_2^n-b^n}{a_2-b}\equiv0\pmod{p}$ гэж гарна.
Одоо $a_1^n-b^n\not\equiv0\pmod{p^2}$ эсвэл $a_2^n-b^n\not\equiv0\pmod{p^2}$ гэж баталъя. Эсрэгээс нь худал гэвэл $$\left\{\begin{array}{l} a_1^n-b^n\equiv0\pmod{p^2}\\ a_2^n-b^n\equiv0\pmod{p^2} \end{array}\right.\Rightarrow a_1^n-a_2^n\equiv0\pmod{p^2}$$ буюу \begin{align*} (g^{4k}b+p^2\ell)^n-\Bigl((p-g)^{4k}b+p^2\ell\Bigr)^n & \equiv(g^{4k}b)^n-\Bigl((p-g)^{4k}b\Bigr)^n\\ & \equiv b^n\Bigl(g^{4nk}-(p-g)^{4nk}\Bigr)\equiv0\pmod{p^2}. \end{align*} Энд $(b,p)=1$ гэдгийг анхаарвал \begin{align*} 0&=(p-g)^{p-1}-g^{p-1}\\ &=p^{p-1}-C_{p-1}^1p^{p-2}g+\dots+(-1)^2p^2C_{p-1}^{p-3}g^{p-3}-pC_{p-1}^{p-2}g^{p-2}+g^{p-1}-g^{p-1}\\ &\equiv -p(p-1)g^{p-2}=pg^{p-2}\not\equiv0\pmod{p^2} \end{align*} зөрчил үүслээ, ө.х. $\exists k\in\{1,2\}$, $a_k$ нь $(*)$-ын $(2)$-ыг хангалаа. Үүгээр $(b,\ell)=1$ байх $\ell\in\mathbb N$ бүрийн хувьд $(*)$-г хангах $a_k$-г олж чадаж байгаа ба $(b,\ell)=1$ байх $\ell$ төсгөлгүй олон тул бодлого бодогдов.
Арифметик прогресс дахь Дирихлейн теоремоор $p\equiv1\pmod{4n}$ байх хангалттай их анхны тоо $p$ олдоно. Тэгвэл $(b,p)=1$ гэж үзэж чадна.
$p=4nk+1$ байг. Модул $p$-ийн анхдагч язгуурыг $g\in\mathbb N$ гээд $$\left\{\begin{array}{l} a_1=g^{4k}b+p^2\ell\\ a_2=(p-g)^{4k}b+p^2\ell \end{array}\right.$$ гэе. $(\ell,b)=1$ бол $(a_1a_2,b)=1$ байна, ө.х. $a_1,a_2$ нь $(*)$-ын $(3)$-ыг хангав. Иймд $(\ell,b)=1$ бол $a_1,a_2$-ын аль нэг нь $(*)$-ын $(1)$ ба $(2)$-ыг хангана гэж харуулъя. $$a_1-b=(g^{4k}-1)b+p^2\ell\equiv(g^{4k}-1)b\not\equiv0\pmod{p},$$ $$a_1^n-b^n=(g^{4k}b+p^2\ell)^n-b^n\equiv(g^{4k}b)^n-b^n\equiv b^n(g^{4nk}-1)\equiv b^n(g^{p-1}-1)\equiv0\pmod{p}.$$ Эндээс $\dfrac{a_1^n-b^n}{a_1-b}\equiv0\pmod{p}$, ө.х. $(*)$-ын $(1)$ биелэв.
$p=4s+1$ хэлбэртэй тул МК-1, \S1.6 дасгал 11-ээр $p-g$ нь мөн модул $p$-ээр анхдагч язгуур учир $\dfrac{a_2^n-b^n}{a_2-b}\equiv0\pmod{p}$ гэж гарна.
Одоо $a_1^n-b^n\not\equiv0\pmod{p^2}$ эсвэл $a_2^n-b^n\not\equiv0\pmod{p^2}$ гэж баталъя. Эсрэгээс нь худал гэвэл $$\left\{\begin{array}{l} a_1^n-b^n\equiv0\pmod{p^2}\\ a_2^n-b^n\equiv0\pmod{p^2} \end{array}\right.\Rightarrow a_1^n-a_2^n\equiv0\pmod{p^2}$$ буюу \begin{align*} (g^{4k}b+p^2\ell)^n-\Bigl((p-g)^{4k}b+p^2\ell\Bigr)^n & \equiv(g^{4k}b)^n-\Bigl((p-g)^{4k}b\Bigr)^n\\ & \equiv b^n\Bigl(g^{4nk}-(p-g)^{4nk}\Bigr)\equiv0\pmod{p^2}. \end{align*} Энд $(b,p)=1$ гэдгийг анхаарвал \begin{align*} 0&=(p-g)^{p-1}-g^{p-1}\\ &=p^{p-1}-C_{p-1}^1p^{p-2}g+\dots+(-1)^2p^2C_{p-1}^{p-3}g^{p-3}-pC_{p-1}^{p-2}g^{p-2}+g^{p-1}-g^{p-1}\\ &\equiv -p(p-1)g^{p-2}=pg^{p-2}\not\equiv0\pmod{p^2} \end{align*} зөрчил үүслээ, ө.х. $\exists k\in\{1,2\}$, $a_k$ нь $(*)$-ын $(2)$-ыг хангалаа. Үүгээр $(b,\ell)=1$ байх $\ell\in\mathbb N$ бүрийн хувьд $(*)$-г хангах $a_k$-г олж чадаж байгаа ба $(b,\ell)=1$ байх $\ell$ төсгөлгүй олон тул бодлого бодогдов.
6. Нэг компани $2n+1$ ажилтантай бөгөөд тэдгээрийн зарим нь хоорондоо танил байв ($A$ нь $B$-г таньдаг бол $B$ нь $A$-г танина). Аль ч $n$ ажилтанг сонгон авахад үлдэх ажилтнууд дотор тэдгээр ажилтнуудыг бүгдийг таньдаг ажилтан заавал олддог бол компанид бүх ажилтанг таньдаг ажилтан бий гэж батал.
Заавар Бодолт
Заавар.
Бодолт. Хүмүүсээ графын орой болгон хоорондоо танил биш хүмүүсийг ирмэгээр холбосон
$G=G(V,E)$ графыг сонирхъё.
1) Ямар ч $n$ орой авахад тэдэнтэй холбогдоогүй нэг орой олддог
2) Бусад оройнуудтайгаа холбогдоогүй орой олддог, ө.х. тусгаарлагдсан оройтой.
Ингэвэл манай бодлого нь $G$ графын хувьд 1) биелбэл 2) биелэхийг батлахад оршино. Одоо $G=G(V,E)$, $|V|=2n+1$-ийн хувьд 1) биелдэг боловч 2) биелдэггүй (тусгаарлагдсан оройгүй) гэж үзье, ө.х. $G\models1)\not\subset\overline{2)}$.
Хэрэв $G$-д 3 урттай зам олддог бол түүний голын ирмэгийг хасахад гарсан $G'=G(V,E')$ графт мөн л $G'\models1)\not\subset\overline{2)}$.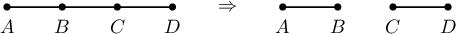
Хэрэв $G$ графт 3 урттай цикл олддог бол түүний нэг ирмэгийг арилгахад гарсан $G'=G(V,E')$ графт мөн л $G'\models1)\not\subset\overline{2)}$ байна.
$G$ графаас дээрх 2 аргаар ирмэгүүдийг хассаар дахин хасах боломжгүй $G_0=G(V,E_0)$ граф гарсан гэвэл $G_0$-ийн холбоост компонентууд нь нэг бол эсвэл
эсвэл
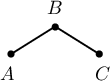 хэлбэртэй байна.
$G_0\models1)\not\subset\overline{2)}$ ба $G_0$ графыг $n$ ба $n+1$ оройтой 2 мөрөнд
байрлуулж
хэлбэртэй байна.
$G_0\models1)\not\subset\overline{2)}$ ба $G_0$ графыг $n$ ба $n+1$ оройтой 2 мөрөнд
байрлуулж
 болох бөгөөд үүний $n$ оройтой мөрийг авахад түүний хувьд 1) үл биелэх, ө.х.
$G_0\models\overline{1)}$ байх нь илэрхий байна.
Үүгээр бид $G_0$ графт $G_0\models1)\not\subset\overline{2)}\not\subset\overline{1)}$ гэсэн зөрчилийг оллоо.
болох бөгөөд үүний $n$ оройтой мөрийг авахад түүний хувьд 1) үл биелэх, ө.х.
$G_0\models\overline{1)}$ байх нь илэрхий байна.
Үүгээр бид $G_0$ графт $G_0\models1)\not\subset\overline{2)}\not\subset\overline{1)}$ гэсэн зөрчилийг оллоо.
$G\models1)\not\subset\overline{2)}$ гэж үзснээс болжээ. Иймд $G\models1)\not\subset 2)$ байна.
1) Ямар ч $n$ орой авахад тэдэнтэй холбогдоогүй нэг орой олддог
2) Бусад оройнуудтайгаа холбогдоогүй орой олддог, ө.х. тусгаарлагдсан оройтой.
Ингэвэл манай бодлого нь $G$ графын хувьд 1) биелбэл 2) биелэхийг батлахад оршино. Одоо $G=G(V,E)$, $|V|=2n+1$-ийн хувьд 1) биелдэг боловч 2) биелдэггүй (тусгаарлагдсан оройгүй) гэж үзье, ө.х. $G\models1)\not\subset\overline{2)}$.
Хэрэв $G$-д 3 урттай зам олддог бол түүний голын ирмэгийг хасахад гарсан $G'=G(V,E')$ графт мөн л $G'\models1)\not\subset\overline{2)}$.
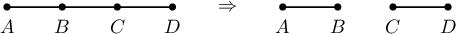
Хэрэв $G$ графт 3 урттай цикл олддог бол түүний нэг ирмэгийг арилгахад гарсан $G'=G(V,E')$ графт мөн л $G'\models1)\not\subset\overline{2)}$ байна.

$G$ графаас дээрх 2 аргаар ирмэгүүдийг хассаар дахин хасах боломжгүй $G_0=G(V,E_0)$ граф гарсан гэвэл $G_0$-ийн холбоост компонентууд нь нэг бол



$G\models1)\not\subset\overline{2)}$ гэж үзснээс болжээ. Иймд $G\models1)\not\subset 2)$ байна.