IMO-47, 12-р анги
Бодлогын тоо: 6 Хугацаа: 540 мин
1. $ABC$ гурвалжинд багтсан тойргийн төв $I$ байг. Уг гурвалжин дотор $P$ цэгийг
$$\angle PBA+\angle PCA=\angle PBC+\angle PCB$$
байхаар авав. $AP\ge AI$ болохыг баталж, тэнцэл болох зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь $P$ цэг $I$-тэй давхцах явдал гэж батал.
Заавар Бодолт
Заавар. $$\angle PBA+\angle PCA=\angle PBC+\angle PCB$$
ба
\begin{align*}
\angle PBA&=\angle IBA-\angle IBP\\
\angle PCA&=\angle ICA+\angle ICP\\
\angle PBC&=\angle IBA+\angle IBC\\
\angle PCB&=\angle ICB-\angle ICP
\end{align*}
тул
$$\angle IBA-\angle IBP+\angle ICA+\angle ICP=\angle IBA+\angle IBC+\angle ICB-\angle ICP$$
болно.
$$\angle IBA+\angle ICA=\angle IBC+\angle ICB$$
болохыг тооцвол
$$-\angle IBP+\angle ICP=\angle IBA-\angle ICP\Rightarrow \angle ICP=\angle IBP$$
болно. Иймд $P$ цэг $BCI$ гурвалжныг багтаасан тойрог дээр байна.
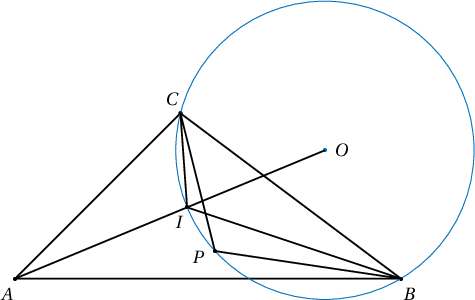

Бодолт. Одоо $BCI$ гурвалжныг багтаасан тойргийн төв $O$ нь $AI$ цацраг дээр оршихыг батлахад хангалттай.
Комплекс хавтгайд $A(a)$, $B(b)$, $C(c)$, $I\equiv 0$ гэе. $I$ биссектриссүүдийн огтлолцолын цэг тул $$\arg\dfrac{c-b}{0-b}=\arg\dfrac{0-b}{a-b},\ \arg\dfrac{b-c}{0-c}=\arg\dfrac{0-c}{a-c}$$ буюу $$\dfrac{c-b}{0-b}:\dfrac{0-b}{a-b}\in\mathbb R, \dfrac{b-c}{0-c}:\dfrac{0-c}{a-c}\in\mathbb R$$ болно. Эндээс $$\left\{\begin{array}{c} \dfrac{(c-b)(a-b)}{b^2}=\dfrac{(\overline{c\vphantom{b}}-\overline{b})(\overline{a\vphantom{b}}-\overline{b})}{\overline{b^2}}\\ \dfrac{(b-c)(a-c)}{c^2}=\dfrac{(\overline{b}-\overline{c\vphantom{b}})(\overline{a\vphantom{b}}-\overline{c\vphantom{b}})}{\overline{c^2}} \end{array} \right.$$ $$\left\{\begin{array}{c} \overline{b^2}(c-b)a-b^2(\overline{c\vphantom{b}}-\overline{b})\overline{a\vphantom{b}}=\overline{b^2}(c-b)b-b^2(\overline{c\vphantom{b}}-\overline{b})\overline{b}\\ \overline{c^2}(b-c)a-c^2(\overline{b}-\overline{c\vphantom{b}})\overline{a\vphantom{b}}=\overline{c^2}(b-c)c-c^2(\overline{b}-\overline{c\vphantom{b}})\overline{c\vphantom{b}} \end{array} \right.$$ $$\left\{\begin{array}{c} \overline{b^2}(c-b)a-b^2(\overline{c\vphantom{b}}-\overline{b})\overline{a\vphantom{b}}=b\overline{b}(\overline{b}c-b\overline{c\vphantom{b}})\\ \overline{c^2}(b-c)a-c^2(\overline{b}-\overline{c\vphantom{b}})\overline{a\vphantom{b}}=c\overline{c\vphantom{b}}(\overline{c\vphantom{b}}b-c\overline{b}) \end{array} \right.$$ $$\Rightarrow a=\dfrac{c^2b\overline{b}(\overline{b}c-b\overline{c\vphantom{b}})+b^2c\overline{c\vphantom{b}}(\overline{c\vphantom{b}}b-c\overline{b})}{c^2\overline{b^2}(c-b)+b^2\overline{c^2}(b-c)}=\dfrac{bc(c\overline{b}-b\overline{c\vphantom{b}})}{(c\overline{b}+b\overline{c\vphantom{b}})(c-b)}$$ $BCI$ гурвалжныг багтаасан тойргийн төвийн координат нь $$z_0=\dfrac{0\overline{0}(b-c)+b\overline{b}(c-0)+c\overline{c\vphantom{b}}(0-b)}{\begin{vmatrix} 1 & 1 & 1\\ 0 & b & c\\ 0 & \overline{b} & \overline{c\vphantom{b}} \end{vmatrix}}=\dfrac{bc(\overline{b}-\overline{c\vphantom{b}})}{b\overline{c\vphantom{b}}-c\overline{b}}$$ $A$, $I$, $O$ цэгүүд нэг шулуун дээр орших зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь $$\dfrac{a}{z_0}=\dfrac{\overline{a}}{\overline{z_0}}$$ байна. Энэ нь $$\dfrac{a}{z_0}=\dfrac{\dfrac{bc(c\overline{b}-b\overline{c\vphantom{b}})}{(c\overline{b}+b\overline{c\vphantom{b}})(c-b)}}{\dfrac{bc(\overline{b}-\overline{c\vphantom{b}})}{b\overline{c\vphantom{b}}-c\overline{b}}}=\dfrac{(b\overline{c\vphantom{b}}-c\overline{b})^2}{(b\overline{c\vphantom{b}}+c\overline{b})(b-c)(\overline{b}-\overline{c\vphantom{b}})}$$ ба $$\overline{b\overline{c\vphantom{b}}-c\overline{b}}=-(b\overline{c\vphantom{b}}-c\overline{b}),\ \overline{b\overline{c\vphantom{b}}+c\overline{b}}=b\overline{c\vphantom{b}}+c\overline{b},$$ $$\overline{(b-c)(\overline{b}-\overline{c\vphantom{b}})}=(\overline{b}-\overline{c\vphantom{b}})(b-c)$$ гэдгээс батлах зүйл мөрдөн гарна.
Комплекс хавтгайд $A(a)$, $B(b)$, $C(c)$, $I\equiv 0$ гэе. $I$ биссектриссүүдийн огтлолцолын цэг тул $$\arg\dfrac{c-b}{0-b}=\arg\dfrac{0-b}{a-b},\ \arg\dfrac{b-c}{0-c}=\arg\dfrac{0-c}{a-c}$$ буюу $$\dfrac{c-b}{0-b}:\dfrac{0-b}{a-b}\in\mathbb R, \dfrac{b-c}{0-c}:\dfrac{0-c}{a-c}\in\mathbb R$$ болно. Эндээс $$\left\{\begin{array}{c} \dfrac{(c-b)(a-b)}{b^2}=\dfrac{(\overline{c\vphantom{b}}-\overline{b})(\overline{a\vphantom{b}}-\overline{b})}{\overline{b^2}}\\ \dfrac{(b-c)(a-c)}{c^2}=\dfrac{(\overline{b}-\overline{c\vphantom{b}})(\overline{a\vphantom{b}}-\overline{c\vphantom{b}})}{\overline{c^2}} \end{array} \right.$$ $$\left\{\begin{array}{c} \overline{b^2}(c-b)a-b^2(\overline{c\vphantom{b}}-\overline{b})\overline{a\vphantom{b}}=\overline{b^2}(c-b)b-b^2(\overline{c\vphantom{b}}-\overline{b})\overline{b}\\ \overline{c^2}(b-c)a-c^2(\overline{b}-\overline{c\vphantom{b}})\overline{a\vphantom{b}}=\overline{c^2}(b-c)c-c^2(\overline{b}-\overline{c\vphantom{b}})\overline{c\vphantom{b}} \end{array} \right.$$ $$\left\{\begin{array}{c} \overline{b^2}(c-b)a-b^2(\overline{c\vphantom{b}}-\overline{b})\overline{a\vphantom{b}}=b\overline{b}(\overline{b}c-b\overline{c\vphantom{b}})\\ \overline{c^2}(b-c)a-c^2(\overline{b}-\overline{c\vphantom{b}})\overline{a\vphantom{b}}=c\overline{c\vphantom{b}}(\overline{c\vphantom{b}}b-c\overline{b}) \end{array} \right.$$ $$\Rightarrow a=\dfrac{c^2b\overline{b}(\overline{b}c-b\overline{c\vphantom{b}})+b^2c\overline{c\vphantom{b}}(\overline{c\vphantom{b}}b-c\overline{b})}{c^2\overline{b^2}(c-b)+b^2\overline{c^2}(b-c)}=\dfrac{bc(c\overline{b}-b\overline{c\vphantom{b}})}{(c\overline{b}+b\overline{c\vphantom{b}})(c-b)}$$ $BCI$ гурвалжныг багтаасан тойргийн төвийн координат нь $$z_0=\dfrac{0\overline{0}(b-c)+b\overline{b}(c-0)+c\overline{c\vphantom{b}}(0-b)}{\begin{vmatrix} 1 & 1 & 1\\ 0 & b & c\\ 0 & \overline{b} & \overline{c\vphantom{b}} \end{vmatrix}}=\dfrac{bc(\overline{b}-\overline{c\vphantom{b}})}{b\overline{c\vphantom{b}}-c\overline{b}}$$ $A$, $I$, $O$ цэгүүд нэг шулуун дээр орших зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь $$\dfrac{a}{z_0}=\dfrac{\overline{a}}{\overline{z_0}}$$ байна. Энэ нь $$\dfrac{a}{z_0}=\dfrac{\dfrac{bc(c\overline{b}-b\overline{c\vphantom{b}})}{(c\overline{b}+b\overline{c\vphantom{b}})(c-b)}}{\dfrac{bc(\overline{b}-\overline{c\vphantom{b}})}{b\overline{c\vphantom{b}}-c\overline{b}}}=\dfrac{(b\overline{c\vphantom{b}}-c\overline{b})^2}{(b\overline{c\vphantom{b}}+c\overline{b})(b-c)(\overline{b}-\overline{c\vphantom{b}})}$$ ба $$\overline{b\overline{c\vphantom{b}}-c\overline{b}}=-(b\overline{c\vphantom{b}}-c\overline{b}),\ \overline{b\overline{c\vphantom{b}}+c\overline{b}}=b\overline{c\vphantom{b}}+c\overline{b},$$ $$\overline{(b-c)(\overline{b}-\overline{c\vphantom{b}})}=(\overline{b}-\overline{c\vphantom{b}})(b-c)$$ гэдгээс батлах зүйл мөрдөн гарна.
2. Зөв $2006$ өнцөгт $P$-ийн диагоналын төгсгөлийн цэгүүд нь $P$-ийн хилийг тус бүр сондгой тооны тал агуулах хоёр хэсэгт хувааж байвал түүнийг сайн гэе. $P$-ийн талуудыг мөн сайн гэе. Аль ч хоёр нь $P$-ийн дотор ерөнхий цэггүй байх $2003$ диагоналаараа $P$ гурвалжнуудад хуваагдсан байг. Тийм хуваалтад хоёр сайн талтай адил хажуут гурвалжин хамгийн олондоо хэд байж болох вэ?
Заавар Бодолт
Заавар. Consider a 2n-gon P. To simplify notation, draw the
circumcircle of P. For a side AB in a triangle ABC, “arc AB” will
denote the arc of the circumcircle not containing C. Arc AB is a
“good arc” if AB is odd in a good triangle ABC.
Consider a side XY of P. Let AB denote the smallest good arc containing vertices X and Y, if it exists. (Note that {A, B} may be equal to {X, Y}.) Let C be the third vertex of the good triangle ABC. Then we will map XY to ABC: f(XY) = ABC.
Consider a side XY of P. Let AB denote the smallest good arc containing vertices X and Y, if it exists. (Note that {A, B} may be equal to {X, Y}.) Let C be the third vertex of the good triangle ABC. Then we will map XY to ABC: f(XY) = ABC.
Бодолт.
3. Аливаа $a$, $b$, $c$ бодит тоонуудын хувьд
$$|ab(a^2-b^2)+bc(b^2-c^2)+ca(c^2-a^2)|\le M(a^2+b^2+c^2)^2$$
тэнцэтгэл биш биелэх байх хамгийн бага бодит тоо $M$-г ол.
4. $$1+2^x+2^{2x+1}=y^2$$
байх бүхэл тооны бүх хос $(x,y)$-г ол.
5. $P(x)$ бүхэл коэффициенттэй $n>1$ зэргийн олон гишүүнт ба $k$ нь натурал тоо байг.
$$Q(x) = P(P(\ldots P(P(x))\ldots))$$
олон гишүүнт авъя (энд $P$ яг $k$ удаа орсон). $Q(t)=t$ байх $t$ бүхэл тоо $n$-ээс илүүгүй оршин байхыг батал.
6. Гүдгэр олон өнцөгт $P$-ийн $b$ тал бүрд, нэг тал нь $b$-тэй давхцах $P$-д агуулагдах гурвалжнуудын талбайн хамгийн ихийг харгалзуулъя. $P$-ийн бүх талуудад харгалзах талбайнуудын нийлбэр, $P$-ийн талбайг хоёр дахин авснаас багагүй гэж батал.