IMO-60, 12-р анги

IMO-60, 2019, Англи   

Бодлогын тоо: 6    Хугацаа: 540 мин

1. Бүхэл тоон олонлогийг $\mathbb Z$ гэж нэрлэе. Дурын бүхэл $a$, $b$ тоонуудын хувьд $$f(2a)+2f(b)=f(f(a+b))$$ байх бүх $f\colon\mathbb Z\to \mathbb Z$ функцийг ол.

Заавар Бодолт
Заавар. $a+b$ нь тогтмол байх утгуудыг ашиглан шугаман функц гэдгийг нь харуул.

Бодолт. $a\to 0$, $b\to n$ гэвэл $$f(0)+2f(n)=f(f(n))$$ $a\to 1$, $b\to n-1$ гэвэл $$f(2)+2f(n-1)=f(f(n))$$ болно. Эндээс $$f(n)=f(n-1)+\dfrac{f(2)-f(0)}{2}$$ болно. Эндээс $f(n)=f(0)+\dfrac{f(2)-f(0)}{2}\cdot n$, $n\in\mathbb Z$ буюу $f(n)=pn+q$, $p=\dfrac{f(2)-f(0)}{2}$, $q=f(0)$ болно. Үүнийг анхны тэгшитгэлд орлуулбал $$f(2a)+2f(b)=f(f(a+b))\Leftrightarrow$$ $$2pa+q+2(pb+q)=p(p(a+b)+q)+q\Leftrightarrow$$ $$2p(a+b)+3q=p^2(a+b)+pq+q$$ нь $\forall a$, $b\in\mathbb Z$ тоонуудын хувьд биелэнэ. Эндээс $p=0$ эсвэл $p=2$ гэж гарах ба $p=0$ үед $q=0$ ба $p=2$ үед $q$ нь дурын бүхэл тоо байж болно. Иймд $$f(x)=0\lor f(x)=2x+q,\ q\in\mathbb Z$$ гэсэн шийдүүдтэй.

2. $ABC$ гурвалжны $BC$ тал дээр $A_1$ цэг, $AC$ тал дээр $B_1$ цэг байрлана. $AA_1$ хэрчим дээрх $P$ цэг ба $BB_1$ хэрчим дээрх $Q$ цэгийн хувьд $PQ$ нь $AB$ шулуунтай параллел болог. $PB_1$ шулуун дээрх $P_1$ цэгийн хувьд $B_1$ цэг $P$, $P_1$ цэгүүдийн хооронд эдгээртэй давхцахгүйгээр байрлах бөгөөд $\angle PP_1C=\angle BAC$ байдаг гэе. Мөн ижлээр, $QA_1$ шулуун дээрх $Q_1$ цэгийн хувьд $A_1$ цэг $Q$, $Q_1$ цэгүүдийн хооронд эдгээртэй давхцахгүйгээр байрлах бөгөөд $\angle CQ_1Q=\angle CBA$ байдаг гэе. $P$, $Q$, $P_1$, $Q_1$ цэгүүд нэг тойрог дээр оршихыг батал.

Заавар Бодолт
Заавар.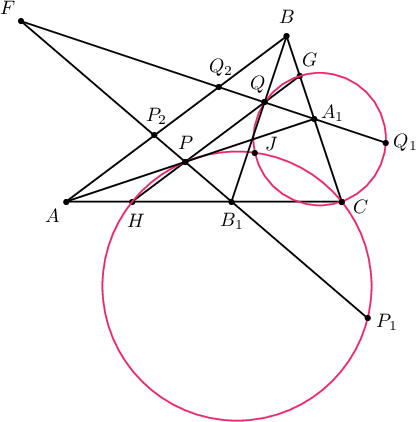


Бодолт. Бодлогын нөхцөлөөс \begin{gather*} GA_1\cdot A_1C=QA_1\cdot A_1Q_1\\ HB_1\cdot B_1C=PB_1\cdot B_1P_1\\ \dfrac{CG}{GB}=\dfrac{CH}{HA}\\ \dfrac{A_1G}{GB}=\dfrac{A_1Q}{QQ_2}=\dfrac{A_1P}{OA}\\ \dfrac{B_1H}{HA}=\dfrac{B_1P}{PP_2}=\dfrac{B_1Q}{QB}\\ \dfrac{FQ_2}{FQ}=\dfrac{FP_2}{FP}\\ \dfrac{FQ_2}{Q_2Q}=\dfrac{FP_2}{P_2P}\\ \end{gather*} \begin{align*} FP\cdot FP_1&= \end{align*}

3. Нийт 2019 хэрэглэгчтэй нэгэн сошиал сүлжээний зарим хэрэглэгчид нь найзууд байв. Сүлжээнд $A$ хэрэглэгч $B$ хэрэглэгчтэй найз бол $B$ хэрэглэгч $A$ хэрэглэгчтэй найз байдаг. Дараах үйл явдал давтагдан, хоёр үйл явдал нэгэн зэрэг биш, явагдах боломжтой:

$A$ нь $B$, $C$-тэй хоёулантай нь найз, харин $B$, $C$ хоорондоо найз биш байдаг $A$, $B$, $C$ гурван хэрэглэгч найзлалтын төлөвөө $B$, $C$ хоорондоо найз, харин $A$ нь $B$-тэй ч найз биш, $C$-тэй ч найз биш байхаар өөрчилнө. Бусад найзлалтын төлөвт өөрчлөлт орохгүй.

Анх $1010$ хэрэглэгч нь тус бүр $1009$ найзтай ба $1009$ хэрэглэгч нь тус бүр $1010$ найзтай бав. Бүх хэрэглэгч нэгээс олонгүй найзтай үлдэх үйл явдлын дараалал олдохыг батал.

4. Дараах нөхцөлийг хангах бүх $(k,n)$ эерэг бүхэл тоон хосыг ол. $$k!=(2^n-1)(2^n-2)(2^n-4)\dots(2^n-2^{n-1})$$

5. Батт Банкнаас гаргадаг зоос нэг талдаа $H$, нөгөө талдаа $T$ үсэгтэй. Номин зүүнээс баруун тийш жагсаасан $n$ ширхэг зоостой. Тэр дараах үйлдлийг давтан хийдэг: хэрэв яг $k>0$ ширхэг зоосны $H$ тал нь дээшээ харсан бол зүүн талаасаа тоолоод $k$ дахь зоосыг эргүүлнэ; үгүй бол бүх зоосны $T$ тал нь дээшээ харсан бөгөөд Номин үйлдэл хийхээ зогсоно. Жишээлбэл, $n=3$ үед анх $THT$ байрлалаас эхлэхэд $THT\to HHT\to HTT\to TTT$ гээд гурван үйлдлийн дараа зогсоно.
  1. Ямар ч байрлалаас эхэлсэн, Номин төгсгөлөг алхамын дараа зогсохыг батал.
  2. Анх $C$ байрлалаас эхлэхэд зогсох хүртэлх үйлдлийн тоог $L(C)$ гэе. Жишээлбэл $L(THT)=3$ ба $L(TTT)=0$ байна. $C$ нь бүх боломжит $2^n$ байрлалаар гүйх үеийн $L(C)$ тоонуудын арифметик дунджийг ол.

6. $AB\neq AC$ байдаг хурц өнцөгт $ABC$ гурвалжинд багтсан $I$ төвтэй $\omega$ тойрог $BC$, $CA$, $AB$ талуудыг, харгалзан, $D$, $E$, $F$ цэгүүдэд шүргэнэ. $D$ цэгийг дайрсан $EF$ шулуунд перпендикуляр шулуун $\omega$ тойргийг дахин $R$ цэгт огтолно. $AR$ шулуун $\omega$ тойргийг дахин $P$ цэгт огтолно. $PCE$, $PBF$ гурвалжнуудыг багтаасан тойргууд дахин $Q$ цэгт огтлолцоно. $DI$ ба $PQ$ шулуунууд $A$ цэгийг дайрсан $AI$ шулуунтай перпендикуляр шулуун дээр огтлолцохыг батал.