Заавар.

Бодолт. $n=2$ үед дурын $ABCD$ дөрвөн өнцөгтийн дотор орших диагональ олдоно гэж баталхад хангалттай. Дөрвөн өнцөгт гүдгэр үед илэрхий. Хотгор үед $\angle A$ өнцгийг хурц гэвэл $AC$ диагональ түүний дотор оршино.

Одоо $n \ge 3$ үед тийм диагоналийг агуулаагүй $2n$ өнцөгт олдоно гэж батлая. $A$ цэгээс $\omega$ тойрогт $AB$, $AC$ шүргэгчүүд татаад $A$ цэгтэй ойр $BC$ нум дээр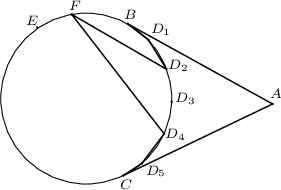 дурын ялгаатай $D_1, D_2, \ldots, D_{2n-3}$ цэгүүдийг энэ дарааллаар авъя. $AD_{n-2}$ шулуун ($AD_{n-1}$ нь гол диагональ юм) $\omega$ тойргийг дахин $E$ цэгээр огтлодог гээд $D_{n-2}$ цэгийг агуулаагүй $BE$ нум дээр $F$ цэг сонгоё. Тэгвэл $$ABD_1D_2\ldots D_{n-2}FD_{n}D_{n+1} \ldots D_{2n-3}C$$ олон өнцөгт тийм диагональ агуулахгүй болж батлагдана. Зурагт $n = 4$ үеийг үзүүлэв.

Заавар.

Бодолт. $A$ цэгийг дайрсан $BL$ шулуунтай параллел шулуун $TL$ шулууныг $E$ цэгт, $B$ цэгийг дайрсан $TL$ шулуунтай параллель шулуун $AE$ шулууныг $F$ цэгт огтолдог байг. $\angle BKM= \angle BAC$ ба $\angle CBL= \angle ALT$ гэдгээс $\triangle ATL \sim \triangle KSB$ төсөөтэй байна. Эндээс $\angle ETA=\angle DSK$ гэж гарна. 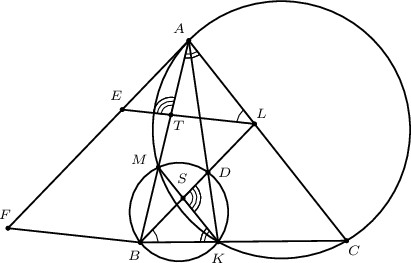Мөн $AF \parallel BL$ тул $$\angle EAM= \angle MBD=\angle MKD$$ болно. Иймд $$\triangle ETA\sim \triangle DSK\qquad(\dagger)$$ байна. $ET \parallel FB$ учир $\triangle ETA\sim \triangle FBA$ байна. $\triangle ATL \sim \triangle KSB$ тул $(\dagger)$-с $$\triangle AEL\sim \triangle KDB\qquad(\ddagger)$$ гэж мөрдөн гарна. Одоо $\dfrac{AT}{SD}=\dfrac{AB}{BD}$ гэж харуулъя. $ET\parallel FB$ тул $\dfrac{AT}{ET}=\dfrac{AB}{FB}$ болох ба эндээс $\dfrac{AT}{SD}=\dfrac{ET}{SD}\dfrac{AB}{FB}$ болно. $(\dagger)$ ба $(\ddagger)$-с $\dfrac{ET}{SD}=\dfrac{EL}{BD}$ тул $$\dfrac{AT}{SD}=\dfrac{EL}{BD}\cdot \dfrac{AB}{FB}$$ гэж гарах бөгөөд $EBFL$ параллелограмм болохыг санавал $\dfrac{AT}{SD}=\dfrac{AB}{BD}$ болж батлагдав.

Заавар.

Бодолт. $n=2\cdot 7^{k-1}$ үед $1 + 2^n + 3^n \equiv 0\pmod{7^k}$ болохыг баталья. $3\equiv -4 \pmod{7}$ учраас зэргийг өргөх леммээр ямар ч натурал $i\geq 1$ тооны хувьд $3^{7^{i-1}}\equiv -4^{7^{k-1}} \pmod{7^i}$ биелнэ. Иймд $3^n \equiv 4^n \pmod{7^k}$ болох тул $1 + 2^n + 4^n\equiv 0\pmod{7^k}$ гэж үзүүлэхэд хангалттай.

$2^3\equiv 1 \pmod{7}$ учраас зэргийг өргөх леммээр ямар ч натурал $i\geq 1$ тооны хувьд $2^{3\cdot 7^{i-1}}\equiv 1 \pmod{7^i}$ биелнэ. Иймд \[ (2^n-1)(4^n + 2^n +1)\equiv 0\pmod{7^k}. \] Фермагийн бага теоремоор $2^n\equiv 2^2\pmod{7}$ тул $2^n-1\not\equiv 0\pmod{7}$ болснoор бодлого бодогдов.

Заавар.

Бодолт. $0 \le x, y \le 1$ бол $ x + y \le 1 + xy $ гэдгээс \begin{align*} a_{1} + a_{2} &\le 1 + a_{1}a_{2} \\ a_{1}a_{2} + a_{3} &\le 1 + a_{1}a_{2}a_{3}\\ &\vdots\\ a_{1}a_{2} \dots a_{n-1} +a_{n} &\le 1 + a_{1}a_{2} \dots a_{n} \end{align*} болох ба бүгдийг нь нэмбэл \begin{equation*} a_{1} + a_{2} + \dots + a_{n} \le (n - 1) + a_{1} a_{2} \dots a_{n} \end{equation*} болно. Энд $s = a_{1} + a_{2} + \dots a_{n}$ ба $p = a_{1} a_{2} \dots a_{n}$ гэвэл $1 + s \le n + p$ болох ба $0 \le p \le 1$ тул \begin{equation*} (1 - p)(1 + s) \le (1 - p)(n + p) = n - (n -1)p - p^{2} \le n \end{equation*} болж бодлого бодогдлоо. Тэнцэтгэл аль нэг нь $0$, бусад нь $1$ үед биелнэ.

Заавар.

Бодолт. $n(P)\le 20$ гэж баталъя. $20\times 20$ хүснэгтийн дурын 1 мөрийг авч үзье. Одоо энэ мөрөнд $0$ юмуу $1$ ширхэг хар нүд байвал шууд бүхэлд нь 1 тэгш өнцөгт болгоё. Харин түүнээс олон тэгш тооны хар нүдтэй бол бүх нүднүүдээ 2 хар нүдтэй тэгш өнцөгтүүдэд хувааж чадна, эсвэл сондгой тооны хар нүдтэй бол баруун захын нүднээс баруун талын бүх нүднүүдээ 1 тэгш өнцөгт болгоод үлдсэн нүднүүдийг 2, 2 хар нүдтэй тэгш өнцөгтүүдэд хувааж чадна. Иймд 1 мөрийг 1-ээс олонгүй хар нүдтэй тэгш өнцөгтүүдэд хувааж чадна. Нийт 20 мөр байх тул хамгийн олондоо 20 байна.

Зураг дээрх тоо бичигдсэн нүднүүдийг хараар будвал бодлогын нөхцөл хангахыг баталъя. Аль ч хоёр 1 гэсэн нүд хамт 1 тэгш өнцөгтөд орж чадахгүй, мөн адилаар аль ч хоёр 2 гэсэн нүд хамт 1 тэгш өнцөгтөд орж чадахгүй. Иймд 1 ба 2 гэсэн нүднүүд цугтаа нэг хүснэгтэнд орж 2 хар нүдтэй болно. Иймд 38 ширхэг 1 гэсэн нүд, 18 ширхэг 2 гэсэн нүд байгаа тул хамгийн олондоо 18 ширхэг 2 хар нүдтэй тэгш өнцөгт байна. Эндээс үлдсэн 20 ширхэг 1 гэсэн нүднүүд бүгдээрээ 1, 1-ээрээ тэгш өнцөгтөд орох тул $n(P)=20$ байна.

Заавар.

Бодолт. $\omega$ тойрог $AB$, $BC$, $CD$, $DA$ талуудыг харгалзан $M$, $N$, $K$, $L$ цэгүүдэд шүргэх ба $T=MN \cap KL$, $S=BD \cap PQ$ гэе. $\omega$ тойргийн хувьд $Z$ цэгийн поляр шулууныг $\ell_Z$ гэж тэмдэглэе. Тэгвэл $T \in \ell_B$ ба $T \in \ell_D$ тул $B \in \ell_T$ ба $D\in \ell_T$ байна. Эндээс $\ell_T=BD$ буюу $IT \perp BD$ болно. Яг адил $E=NC\cap ML$ гэвэл $\ell_E=AC$ болох ба $T\in \ell_E$ тул $T \in AC$ байна. Эндээс $(QTPS)$ гармоник тул $I(QTPS)$ харандаа болно.

$\omega$ тойрог ба $PBD$, $QBD$ гурвалжнуудын радиус нь $r$, $r_1$, $r_2$ байг. $S'=XY \cap PQ$ гэвэл $IPQ$ гурвалжны хувьд Менелайн теоремоор $\dfrac{IP}{XP}\cdot\dfrac{XS'}{YS'}\cdot\dfrac{YQ}{IQ}=1$ байна. Нөгөө талаас $\dfrac{IP}{XP}=\dfrac{r}{r_1}$ ба $\dfrac{YQ}{IQ}=\dfrac{r_2}{r}$ гэдгээс $\dfrac{XS'}{YS'}=\dfrac{r_1}{r_2}$ болох тул $S=S'$ болно. Эндээс $Z=IT \cap XY$ гэвэл $I(QTPS)$ харандаа тул $(YZXS)$ гармоник буюу $\dfrac{XZ}{YZ}=\dfrac{r_1}{r_2}$ байна. Иймд $IZ$, $PY$, $QX$ шулуунууд нэг цэгт огтлолцоно гэж баталхад хангалттай ба энэ нь $IPQ$ гурвалжны хувьд Чевийн теоремоор дээрх тэгшитгэлийг ашиглаад хялбар батлагдана.