Дүүрэг 2019, Дунд ангийн багш
Бодлогын тоо: 4 Хугацаа: 210 мин
1. $0<\alpha,\beta,\gamma<\dfrac{\pi}{2}$ бол
$$\dfrac{\alpha\cos\alpha+\beta\cos\beta+\gamma\cos\gamma}{\alpha+\beta+\gamma}\le\dfrac{\cos\alpha+\cos\beta+\cos\gamma}{3}$$
тэнцэтгэл биш биелэхийг батал.
Заавар Бодолт
Заавар. Косинус нь $[0,\pi/2]$ завсарт буурах функц ба Чебышевийн тэнцэтгэл биш ашигла.
Бодолт. $\alpha\le\beta\le\gamma$ бол $\cos\alpha\ge\cos\beta\ge\cos\gamma$ байна. Эдгээр тоонууд дээр Чебышевийн тэнцэтгэл биш бичвэл
$$\alpha\cos\alpha+\beta\cos\beta+\gamma\cos\gamma\le\dfrac{(\alpha+\beta+\gamma)(\cos\alpha+\cos\beta+\cos\gamma)}{3}$$
болно. Чебышевийн тэнцэтгэл бишийн тэнцэх нөхцөлөөс $\alpha=\beta=\gamma$ үед тэнцэтгэл биш тэнцэлдээ хүрэх нь мөрдөн гарна.
2. $1$, $3$, $4$-ийн цифрүүдээр бичигддэг, цифрүүдийн нийлбэр нь $n$-тэй тэнцүү натурал тоонуудын тоог $a_n$ гэе. Тэгвэл $a_{2n}$ бүтэн квадрат болохыг батал.
Заавар Бодолт
Заавар. $a_1=1$, $a_2=1$, $a_3=2$, $a_4=4$ ба $n>4$ үед
$$a_n=a_{n-1}+a_{n-3}+a_{n-4}$$
байна.
Бодолт. Я. Лхагвагэрэл багшийн ирүүлсэн бодолт.
$a_n$ тооны рекуррент томьёог $a_{2n+2}$, $a_{2+1}$, $a_{2n}$ гишүүдийн хувьд бичвэл \begin{align*} a_{2n+2}&=a_{2n+1}+a_{2n-1}+a_{2n-2}\\ a_{2n+1}&=a_{2n}+a_{2n-2}+a_{2n-3}\\ a_{2n}&=a_{2n-1}+a_{2n-3}+a_{2n-4}\\ \end{align*} байна. Эхний хоёрын нийлбэрээс гурав дахийг хасвал $$a_{2n+2}=2a_{2n}+2a_{2n-2}-a_{2n-4}$$ болно. $x_n=a_{2n}$ гэвэл $$x_{n+1}=2x_n+2x_{n-1}-x_{n-2}$$ биелэнэ. $x_n=F_n^2$ гэж индукцээр баталъя. Энд $F_n$ нь $n$-р Фибоначчийн тоо юм ($F_0=F_1=1$, $F_{n+1}=F_n+F_{n-1}$). $x_1=F_1^2$, $x_2=F_2^2$, $x_3=F_3^2$ болохыг шууд шалгаж болно. Одоо $$x_{n+1}=2F_n^2+2F_{n-1}^2-F_{n-2}^2$$ гэдгээс $F_{n-2}=F_n-F_{n-1}$ гэдгийг тооцвол \begin{align*} x_n&=2F_n^2+2F_{n-1}^2-F_n^2-F_{n-1}^2+2F_{n-1}F_{n}\\ &=F_n^2+2F_nF_{n-1}+F_{n-1}^2=(F_n+F_{n-1})^2=F_n^2 \end{align*} болж батлагдав.
$a_n$ тооны рекуррент томьёог $a_{2n+2}$, $a_{2+1}$, $a_{2n}$ гишүүдийн хувьд бичвэл \begin{align*} a_{2n+2}&=a_{2n+1}+a_{2n-1}+a_{2n-2}\\ a_{2n+1}&=a_{2n}+a_{2n-2}+a_{2n-3}\\ a_{2n}&=a_{2n-1}+a_{2n-3}+a_{2n-4}\\ \end{align*} байна. Эхний хоёрын нийлбэрээс гурав дахийг хасвал $$a_{2n+2}=2a_{2n}+2a_{2n-2}-a_{2n-4}$$ болно. $x_n=a_{2n}$ гэвэл $$x_{n+1}=2x_n+2x_{n-1}-x_{n-2}$$ биелэнэ. $x_n=F_n^2$ гэж индукцээр баталъя. Энд $F_n$ нь $n$-р Фибоначчийн тоо юм ($F_0=F_1=1$, $F_{n+1}=F_n+F_{n-1}$). $x_1=F_1^2$, $x_2=F_2^2$, $x_3=F_3^2$ болохыг шууд шалгаж болно. Одоо $$x_{n+1}=2F_n^2+2F_{n-1}^2-F_{n-2}^2$$ гэдгээс $F_{n-2}=F_n-F_{n-1}$ гэдгийг тооцвол \begin{align*} x_n&=2F_n^2+2F_{n-1}^2-F_n^2-F_{n-1}^2+2F_{n-1}F_{n}\\ &=F_n^2+2F_nF_{n-1}+F_{n-1}^2=(F_n+F_{n-1})^2=F_n^2 \end{align*} болж батлагдав.
3. $x$, $y$, $z$ бүхэл тоонуудын $\text{ХИЕХ}(x,y,z)=1$ бөгөөд
$$y^2z+yz^2=x^3+x^2z-2xz^2$$
тэгшитгэлийн шийд болог. Тэгвэл $z$ - бүтэн куб (бүхэл тооны куб) болохыг батал.
Заавар Бодолт
Заавар. $$x^3=z(y^2+yz+2xz-x^2)$$
гээд $z$ нь тооны куб биш гээд зөрчил үүсгэ.
Бодолт. Я. Лхагвагэрэл багшийн ирүүлсэн бодолт (Facebook-ээс авсан).
$$x^3=z(y^2+yz+2xz-x^2)$$ байна. $z$ нь тооны куб биш гэж үзвэл $z$-ийг хуваадаг, зэрэг нь $3$-д хуваагддаггүй байх $p\in\mathbb P$ тоо олдоно. Тэрхүү $p$-г авч үзье. $$p\mid z\Rightarrow p\mid x^3\Rightarrow p\mid x\Rightarrow x^3=p^{3k}s,\ p\nmid s, k\ge 1$$ байна. $z$ нь тооны куб биш тул $$p\mid y^2+yz+2xz-x^2$$ байна. Энд $p\mid z$, $p\mid x$ гэдгийг тооцвол $p\mid y^2\Rightarrow p\mid y$ болно. Иймд $p\mid(x,y,z)=1$ болж зөрчил үүсэв.
$$x^3=z(y^2+yz+2xz-x^2)$$ байна. $z$ нь тооны куб биш гэж үзвэл $z$-ийг хуваадаг, зэрэг нь $3$-д хуваагддаггүй байх $p\in\mathbb P$ тоо олдоно. Тэрхүү $p$-г авч үзье. $$p\mid z\Rightarrow p\mid x^3\Rightarrow p\mid x\Rightarrow x^3=p^{3k}s,\ p\nmid s, k\ge 1$$ байна. $z$ нь тооны куб биш тул $$p\mid y^2+yz+2xz-x^2$$ байна. Энд $p\mid z$, $p\mid x$ гэдгийг тооцвол $p\mid y^2\Rightarrow p\mid y$ болно. Иймд $p\mid(x,y,z)=1$ болж зөрчил үүсэв.
4. $\omega$ тойрогт $AB$ гипотенузтай $ABC$ тэгш өнцөгт гурвалжин багтжээ. $BC$ нумын ($A$-г агуулаагүй) дундаж цэг $K$,
$AC$ талын дундаж цэг $N$, $KN$ цацрагийн $\omega$ тойрогтой огтлолцох цэг $M$ болно. $\omega$ тойргийн $A$ ба $C$ цэгүүдэд татсан шүргэгч шулуунууд $E$ цэгт огтлолцдог бол $\measuredangle EMK$ өнцгийн хэмжээг ол.
Заавар Бодолт
Заавар. $MOKE$ дөрвөн өнцөгт тойрогт багтана гэж харуул.
Бодолт. Я. Лхагвагэрэл багшийн ирүүлсэн бодолт.
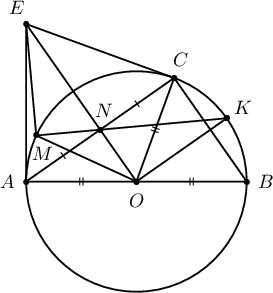Нэг цэгээс татсан шүргэгчүүд тул $AE=EC$, $N\in EO$ ба $EN\perp AC$ ($\measuredangle EOK=90^\circ$) байна. $OC=OB$, $CK=BK$ тул $OK\perp BC$ байна. $NO$ нь $\triangle ABC$-ийн дундаж шугам тул $ON\parallel BC$ ба $OE\perp OK$ байна. $\omega$ тойргийн хувьд
$$MN\cdot NK=AN\cdot NC$$
дөрвөн өнцөгт $AECO$ нь эсрэг өнцгүүд нь $90^\circ$ тул нийлбэр нь $180^\circ$ болж тойрогт багтана. Тэрхүү тойргийг $\omega_1$ гэе. Тэгвэл $\omega_1$-ийн хувьд
$$AN\cdot NC=EN\cdot NO$$
болно. Эндээс
$$MN\cdot NK=EN\cdot NO$$
буюу $MOKE$ дөрвөн өнцөгт тойрогт багтана. Иймд
$$\measuredangle EMK=\measuredangle EOK=90^\circ$$
болж бодлого бодлогдов.