Дүүрэг 2019 Монгол Бодлогын Сан

Дүүрэг 2019, 11-р анги

Бодлогын тоо: 4 Хугацаа: 210 мин

$x$ ,

$y$ ,

$z$ дурын бодит тоонууд бол

$f(x,y,z)=\sqrt{2+x^2}+\sqrt{2+(x-y)^2}+\sqrt{2+(y-z)^2}+\sqrt{2+(2-z)^2}$ илэрхийллийн авч болох хамгийн бага утгыг ол.

Заавар Бодолт

Заавар.

$A(0,0)$ ,

$B(\sqrt{2},x)$ ,

$C(2\sqrt{2},y)$ ,

$D(3\sqrt{2},z)$ ,

$E(4\sqrt{2},2)$ тахир шугамын урт хамгийн багадаа хэдтэй тэнцэх вэ?

Бодолт.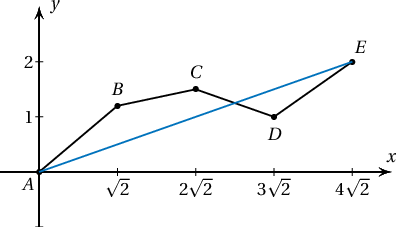

Гурвалжны тэнцэтгэл бишээр

$AB+BC+CD+DE\ge AE$ байна. Нөгөө талаас

$AB=\sqrt{2+x^2}$ ,

$BC=\sqrt{2+(x-y)^2}$ ,

$CD=\sqrt{2+(y-z)^2}$ ,

$DE=\sqrt{2+(2-z)^2}$ тул

$f(x,y,z)=AB+BC+CD+DE$ тул хамгийн бага утга нь

$B$ ,

$C$ ,

$D$ цэгүүд

$AE$ хэрчим дээр орших үед

$AE=\sqrt{2^2+(4\sqrt2)^2}=6$ байна. Энэ үед

$x=\dfrac12$ ,

$y=1$ ,

$z=\dfrac32$ байна.

2. Бүхэл тоо бүрийг улаан эсвэл хөх өнгийн аль нэгээр дурын аргаар будахад өгөгдсөн

$k$ натурал тоонд хуваагддаг, ижил өнгийн төгсгөлгүй олон тоо олдохыг батал.

Заавар Бодолт

Заавар. Төгсгөлгүй олонлогийн элементүүдийг дурын аргаар хоёр хэсэгт хуваахад аль нэг хэсэгт нь төгсгөлгүй олон элемент орно.

Бодолт.

$kn$ ,

$n\in\mathbb Z$ хэлбэрийн тоо төгсгөлгүй олон байна. Эдгээрийг хоёр өнгөөр будахад аль нэг хэсэгт нь төгсгөлгүй олон тоо орно. Эдгээр нь нэг өнгийн,

$k$ тоонд хуваагддаг, төгсгөлгүй олон тоо болно.

$\dfrac{2a^2+3b^2}{2a+3b}$ бүхэл тоо байдаг бүх

$(a,b)$ гэсэн харилцан анхны натурал тоон хосыг ол.

Заавар Бодолт

Заавар.

$2a^2+3b^2=(2a+3b)(a+b)-5ab$ болохыг ашигла.

Бодолт.

$2a^2+3b^2=(2a+3b)(a+b)-5ab$ тул

$\dfrac{2a^2+3b^3}{2a+3b}\in\mathbb Z\Leftrightarrow\dfrac{5ab}{2a+3b}\in\mathbb Z$ болно.

$(a,2a+3b)=(a,3b)=1\lor 3$ бөгөөд

$(b,2a+3b)=(b,2a)=1\lor 2$ болно. Дараах тохиолдлуудыг авч үзье.

$3\nmid a$ , $2\nmid b$ байг. Тэгвэл $2a+3b\mid 5\Rightarrow a=b=1$ .
$a=3m$ , $2\nmid b$ байг. Тэгвэл $2a+3b=6m+3b\mid 5\cdot 3=15\Rightarrow 2m+b\mid 5$ болж $b=1$ , $m=2$ ба $a=6$ болно.
$b=2n$ , $3\nmid a$ байг. Тэгвэл $2a+3b=2a+6n\mid 5\cdot 2=10\Rightarrow a+3n\mid 5$ болж $a=2$ , $n=1$ ба $b=2$ болно. Гэвч энэ нь $(a,b)=1$ гэдэгт зөрчинө.
$a=3m$ ба $b=2n$ байг. Тэгвэл $2a+3b=6m+6n\mid 5\cdot 3\cdot2\Rightarrow m+n\mid 5$ болно. Эндээс $(m,n)=(1,4)$ , $(2,3)$ , $(3,2)$ , $(4,1)$ ба эдгээрт харгалзан $(a,b)=(3,8)$ , $(6,6)$ , $(9,4)$ , $(12,2)$ болно. $(a,b)=1$ байх ёстой. Иймд $(a,b)=(3,8)$ , $(9,4)$ гэсэн шийдүүд олдоно.

$ABC$ тэгш өнцөгт гурвалжны

$\measuredangle B=90^\circ$ болно.

$AA_1$ ба

$CC_1$ биссектрисууд

$I$ цэгт огтлолцоно.

$C_1$ цэгийг дайрсан

$AA_1$ -д перпендикуляр шулуун ба

$A_1$ цэгийг дайрсан

$CC_1$ -д пердендикуляр шулуун

$K$ цэгт огтлолцдог бол

$KI$ хэрчмийн дундаж цэг

$AC$ хэрчим дээр оршихыг батал.

Заавар Бодолт

Заавар.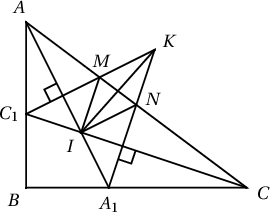

$KC_1\cap AC=M$ ,

$KA_1\cap AC=N$ болог.

$MINK$ нь параллелограмм гэж батлахад хангалттай.

Бодолт.

$C_1AM$ адил хажуут гурвалжин бөгөөд (биссектрис ба өндөр нь давхацсан)

$C_1IM$ мөн

$C_1M$ суурьтай адил хажуут гурвалжин болно.

$\measuredangle AC_1I=\measuredangle AC_1C=180^\circ-\alpha-\dfrac{\gamma}{2}=90^\circ+\dfrac{\gamma}{2},\ \measuredangle AC_1M=90^\circ-\dfrac{\alpha}{2}\Rightarrow$

$\measuredangle AIC_1=\measuredangle AC_1C-\measuredangle AC_1M=90^\circ+\dfrac{\gamma}{2}-90^\circ+\dfrac{\alpha}{2}=45^\circ$ Иймд

$\measuredangle CIM=90^\circ\Rightarrow MI\parallel KA_1$ . Үүнтэй адилаар

$NI\parallel C_1K$ болно. Эндээс

$MINK$ параллелограмм болох тул

$IK$ хэрчмийн дундаж цэг нь

$MN$ хэрчимд агуулдана. Иймд

$IK$ хэрчмийн дундаж цэг нь мөн

$AC$ дээр оршино.

Дүүрэг 2019, 11-р анги

Санал хүсэлт: