МУБИС-ийн олимпиад 2019, 10-р анги
Бодлогын тоо: 4 Хугацаа: 180 мин
1. $a^3\ge12$ ба $abc = 1$ байх $a$, $b$, $c$ бодит тоонуудын хувьд
$$\dfrac{a^2}{2}+b^2 +c^2 \ge ab+bc+ca$$
тэнцэтгэл биш биелэхийг батал.
Заавар Бодолт
Заавар. Бүтэн квадрат ашиглах арга ба $abc=1,\ a^3\ge12\Rightarrow a^2-12bc\ge 0$ тэнцэтгэл бишийг ашигла.
Бодолт. Шинэ-Үе сургуулийн багш Б. Мөнхтулгын ирүүлсэн бодолт.
$a^3\ge 12$ ба $abc=1$ гэдгээс $a^2\cdot a=a^2\cdot\dfrac{1}{bc}\ge12$ буюу $a^2\ge12bc$ буюу $a^2-12bc\ge 0$ тэнцэтгэл биш биелэнэ. $$\dfrac{a^2}{2}+b^2 +c^2 \ge ab+bc+ca\Leftrightarrow \dfrac{a^2}{2}+b^2+c^2-ab-bc-ac\ge0$$ байна. $$\dfrac{a^2}{2}+b^2+c^2-ab-bc-ac=\left(\dfrac{a}{2}-b-c\right)^2+\dfrac{a^2}{4}-8bc=$$ $$=\left(\dfrac{a}{2}-b-c\right)^2+\dfrac{a^2-12bc}{4}\ge0$$ болж батлагдав. Тэнцэтгэлдээ хүрэх нөхцөл нь $a=\sqrt[3]{12}$ ба $b$, $c$ нь $x^2-2ax+\dfrac{a^2}{12}=0$ тэгшитгэлийн ялгаатай шийдүүд юм.
$a^3\ge 12$ ба $abc=1$ гэдгээс $a^2\cdot a=a^2\cdot\dfrac{1}{bc}\ge12$ буюу $a^2\ge12bc$ буюу $a^2-12bc\ge 0$ тэнцэтгэл биш биелэнэ. $$\dfrac{a^2}{2}+b^2 +c^2 \ge ab+bc+ca\Leftrightarrow \dfrac{a^2}{2}+b^2+c^2-ab-bc-ac\ge0$$ байна. $$\dfrac{a^2}{2}+b^2+c^2-ab-bc-ac=\left(\dfrac{a}{2}-b-c\right)^2+\dfrac{a^2}{4}-8bc=$$ $$=\left(\dfrac{a}{2}-b-c\right)^2+\dfrac{a^2-12bc}{4}\ge0$$ болж батлагдав. Тэнцэтгэлдээ хүрэх нөхцөл нь $a=\sqrt[3]{12}$ ба $b$, $c$ нь $x^2-2ax+\dfrac{a^2}{12}=0$ тэгшитгэлийн ялгаатай шийдүүд юм.
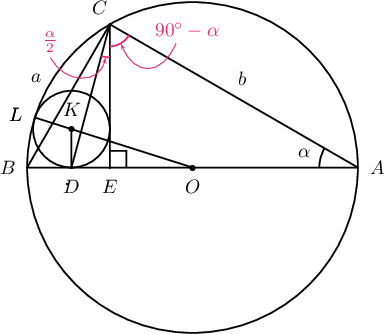
2. $\measuredangle ACB = 90^\circ$ байх тэгш өнцөгт $ABC$ гурвалжны $C$ оройн өндрийн суурь $E$, $\measuredangle ECB$ өнцгийн биссектрис $AB$ талыг $D$ цэгт огтолно. Хэрэв $AB$ талыг $D$ цэгт шүргэх тойрог $CE$ өндрийг шүргэдэг бол энэ тойрог $ABC$ гурвалжныг багтаасан тойргийг шүргэхийг батал.
3. Аливаа натурал $n$ тооны хувьд квадратуудын нийлбэр нь бүхэл тооны 16 зэрэг байх харилцан ялгаатай $n$ ширхэг натурал тоо олдох уу?
4. $X$ олонлогийн элемент бүр нь ядаж $n$ дэд олонлогт агуулагдаж байхаар $X$ олонлогийн дэд олонлогууд өгөгдөв. Хэрэв эдгээр дэд олонлогуудын аль ч 2 нь хамгийн ихдээ 1 ерөнхий элементтэй бол ижил тооны элементтэй $n$ дэд олонлог олдохыг батал.