Сайн гараа 2018, 10-р анги
Бодлогын тоо: 4 Хугацаа: мин
1. $n\ge3$ натурал тоо. Хэрэв $4n+1$ анхны тоо бол $n^{2n}-1$ тоо $4n+1$-д хуваагдахыг батал.
Заавар Бодолт
Заавар. $p=4n+1$ гэвэл $(2,p)=1$ байна. Фермагийн теорем ашигла.
Бодолт. Фермагийн теоремоор $2^{p-1}\equiv 4^{2n}\equiv1\pmod{p}$ байна. Түүнчлэн $n=\dfrac{p-1}{4}$ тул
$$n^{2n}\equiv\left(\dfrac{p-1}{4}\right)^{2n}\equiv 4^{2n}\cdot\left(\dfrac{p-1}{4}\right)^{2n}\equiv (p-1)^{2n}\equiv (-1)^{2n}\equiv1\pmod{p}$$
тул $p\mid n^{2n}-1$ буюу $4n+1\mid n^{2n}-1$ байна.
2. Дурын $n\ge 2$ натурал тоо ба дурын $a_1, a_2,\ldots,a_n$ гэсэн 1-ээс багагүй тоонуудын хувьд
$$\dfrac{a_1+x}{2}\cdot\dfrac{a_2+x}{2}\cdot\cdots\cdot\dfrac{a_n+x}{2}\le\dfrac{a_1a_2\ldots a_n+x}{2}$$
тэнцэтгэл биш биелдэг байх бүх $-1$-ээс багагүй $x$-үүдийг ол.
Заавар Бодолт
Заавар. $a_1=a_2=\dots=a_n=1$ гэвэл $\left(\dfrac{1+x}{2}\right)^n\le\dfrac{1+x}{2}$ болно.
Бодолт. Т. Базарын ирүүлсэн бодолт.
$\left(\dfrac{1+x}{2}\right)^n\le\dfrac{1+x}{2}$ ба $x\ge-1$ тул $\dfrac{x+1}{2}\ge 0$ тул $\dfrac{1+x}{2}\le 1$ буюу $x\le 1$ болно. Одоо $\forall x\in[-1;1]$ ба $\forall a_1,\ldots,a_n$ тоонуудын хувьд $$\dfrac{a_1+x}{2}\cdot\dfrac{a_2+x}{2}\cdot\cdots\cdot\dfrac{a_n+x}{2}\le\dfrac{a_1a_2\ldots a_n+x}{2}$$ гэж батлахад хангалттай. Индукцээр баталъя. $n=2$ үед $$\dfrac{a_1+x}{2}\cdot\dfrac{a_2+x}{2}\le\dfrac{a_1a_2+x}{2}\Leftrightarrow a_1a_2+(2-a_1-a_2)x-x^2\ge 0$$ болно. $x^2\le 1$ ба $2-a_1-a_2\le 0$ тул $(2-a_1-a_2)\le (2-a_1-a_2)x$ байна. Иймд \begin{align*} a_1a_2+(2-a_1-a_2)x-x^2 &\ge a_1a_2+(2-a_1-a_2)-1\\ &=a_1a_2-a_1-a_2+1\\ &=(a_1-1)(a_2-1)\ge 0 \end{align*} болж батлагдав.
$n\to n+1$ индукцийн шилжилт илэрхий юм.
$\left(\dfrac{1+x}{2}\right)^n\le\dfrac{1+x}{2}$ ба $x\ge-1$ тул $\dfrac{x+1}{2}\ge 0$ тул $\dfrac{1+x}{2}\le 1$ буюу $x\le 1$ болно. Одоо $\forall x\in[-1;1]$ ба $\forall a_1,\ldots,a_n$ тоонуудын хувьд $$\dfrac{a_1+x}{2}\cdot\dfrac{a_2+x}{2}\cdot\cdots\cdot\dfrac{a_n+x}{2}\le\dfrac{a_1a_2\ldots a_n+x}{2}$$ гэж батлахад хангалттай. Индукцээр баталъя. $n=2$ үед $$\dfrac{a_1+x}{2}\cdot\dfrac{a_2+x}{2}\le\dfrac{a_1a_2+x}{2}\Leftrightarrow a_1a_2+(2-a_1-a_2)x-x^2\ge 0$$ болно. $x^2\le 1$ ба $2-a_1-a_2\le 0$ тул $(2-a_1-a_2)\le (2-a_1-a_2)x$ байна. Иймд \begin{align*} a_1a_2+(2-a_1-a_2)x-x^2 &\ge a_1a_2+(2-a_1-a_2)-1\\ &=a_1a_2-a_1-a_2+1\\ &=(a_1-1)(a_2-1)\ge 0 \end{align*} болж батлагдав.
$n\to n+1$ индукцийн шилжилт илэрхий юм.
3. Аль ч дараалсан хоёр цифр нь ялгаатай ба сүүлчийн цифр нь анхны тоо байх 2018 оронтой тоо хэчнээн байх вэ?
Заавар Бодолт
Заавар. Бодлогын нөхцөл хангах тоонуудыг $b_n$ гэвэл $b_1=4$
$$b_{n+1}=3\cdot b_n+4\cdot(9^n-b_n)$$
байна.
Бодолт. $b_1=4$ ба $n\ge 1$ үед
$$b_{n+1}=4\cdot 9^n-b_n$$
рекуррент харьцааг бодъё. $c_n=\dfrac{b_n}{9^n}$ гэвэл $c_1=\dfrac{4}{9}$ ба
$$9c_{n+1}=4-c_n$$
$d_n=c_n-\dfrac{2}{5}$ гэвэл $d_1=\dfrac{4}{9}-\dfrac{2}{5}=\dfrac{2}{45}$ ба $d_{n+1}=-\dfrac{1}{9}d_n$ байна. Иймд
$$d_n=\dfrac{2}{45}\cdot\left(-\dfrac19\right)^{n-1}\Rightarrow c_n=(-1)^{n-1}\cdot\dfrac{2}{5}\cdot\dfrac1{9^n}+\dfrac25$$
болох тул
$$b_n=9^n\cdot\left((-1)^{n-1}\cdot\dfrac{2}{5}\cdot\dfrac1{9^n}+\dfrac25\right)=\dfrac25\cdot\left(9^n-(-1)^n\right)$$
байна.
4. $ABC$ гурвалжинд багтсан тойрог $AB$ талыг $D$ цэгт шүргэнэ. $ACD$ гурвалжинд багтсан тойрог $AC$, $AD$ талыг харгалзан $P$, $Q$ цэгт, $DCB$ гурвалжинд багтсан тойрог $BC$, $BD$ талуудыг харгалзан $R$, $S$ цэгүүдэд шүргэдэг $P$, $Q$, $R$, $S$ цэгүүд нэг тойрог дээр оршино гэж батал.
Заавар Бодолт
Заавар. Хоёр багтсан тойрог нь биссектрисээ нэг ижил цэгт шүргэнэ гэдгийг харуул.
$A$ оройгоос багтсан тойрогт татсан шүргэгчийн урт
$$\dfrac{b+c-a}{2}$$
болохыг ашигла.
Бодолт. Т. Базарын ирүүлсэн бодолт.
$CD$ биссектрисийн $ACD$ ба $DCB$ гурвалжнуудад багтсан тойргуудыг шүргэх цэгүүдийг харгалзан $E$, $F$ гэе.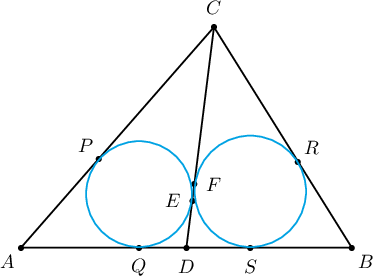
$AD=\dfrac{b+c-a}{2}$, $BD=\dfrac{a+c-b}{2}$ байна. Түүнчлэн
$$DE=\dfrac{CD+AD-b}{2}=\dfrac{CD+\dfrac{b+c-a}{2}-b}{2}=\dfrac{2CD+c-a-b}{4}$$
ба
$$DF=\dfrac{CD+BD-a}{2}=\dfrac{CD+\dfrac{a+c-b}{2}-a}{2}=\dfrac{2CD+c-a-b}{4}$$
тул $E\equiv F$ байна. Иймд $CP=CE=CR$ болох тул
\begin{align*}
\measuredangle PRS&=180^\circ-\measuredangle PRC-\measuredangle SRB\\
&=180^\circ-\dfrac{180^\circ-\gamma}{2}-\dfrac{180^\circ-\beta}{2}=\dfrac{\beta+\gamma}{2}\\
\measuredangle PQS&=\measuredangle APQ+\measuredangle PAQ=90^\circ-\dfrac{\alpha}{2}+\alpha=90^\circ+\dfrac{\alpha}{2}
\end{align*}
буюу
$$\measuredangle PRS+\measuredangle PQS=\dfrac{\beta+\gamma}{2}+90^\circ+\dfrac{\alpha}{2}=180^\circ$$
болно. Иймд $PQRS$ багтсан дөрвөн өнцөгт болно.
$CD$ биссектрисийн $ACD$ ба $DCB$ гурвалжнуудад багтсан тойргуудыг шүргэх цэгүүдийг харгалзан $E$, $F$ гэе.