Бага сунгаа V, Дунд ангийн багш
Бодлогын тоо: 4 Хугацаа: 180 мин
1. $ad=bc$ ба $n^2 < a < b < c < d < (n+1)^2$ байх $a$, $b$, $c$, $d\in\mathbb N$ тоонууд олдохгүй гэж батал.
Заавар Бодолт
Заавар.
Бодолт. Эсрэгээс нь $ad=bc$ байх $a$, $b$, $c$, $d\in\mathbb N$ олддог гэе.
$$d-a<(n+1)^2-(n^2+1)<2n$$
байх нь илэрхий.
$$a(a+d-b-c)=a^2+ad-ab-ac=a^2+bc-ab-ac=$$
$$=(b-a)(c-a)>0$$
тул $a+d-b-c>0$ буюу $a+d>b+c$ гэж гарна.
$$(d+a)^2-(d-a)^2=4ad=4bc<(b+c)^2$$
гэдгээс
$$(d-a)^2>(d+a)^2-(b+c)^2=$$
$$=(a+b+c+d)(a+d-b-c)>a+b+c+d>4n^2$$
буюу
$$d-a>2n$$
болж зөрчилд хүрэв.
2. $n\times n$ хүснэгтэд $2n-2$ тэмээг бие биеээ идэхгүйгээр хэчнээн янзаар байрлуулж болох вэ?
Заавар Бодолт
Заавар. $n\times n$ хүснэгтэд $2n-2$ тэмээг бие биеээ идэхгүйгээр байрлуулсан бол бүх тэмээ захын нүдэнд байрлахыг харуул.
Бодолт. Хоёр гол диагонал дээр 1, 1 л тэмээ байрлах тул булангийн нүднүүд дээр хамгийн ихдээ 2 л тэмээ байрлах боломжтой. Эсрэг булангуудын аль нэг дээр тэмээ байрлахгүй бол $2n-2$ тэмээ байрлах боломжгүй. Учир нь $n\times n$ хүснэгтийг $2n-1$ параллел диагоналд хувааж болох бөгөөд эдгээрийн хоёр дээр нь (эсрэг булангууд дээр) тэмээ байрлаагүй тохиолдолд хамгийн ихдээ $2n-3$ тэмээ л байрлах боломжтой юм. Иймд буланд яг 2 ширхэг тэмээ байрлах ба булан диагоналаас бусад бүх диагонал дээр тэмээ байрлана.
Одоо бүх тэмээ хүснэгтийн захын нүдэнд (хамгийн цөөн нүүдэлтэй нүднүүд) байрлах ёстойг харуулъя. $x$ нүд ба $x$ нүдийг агуулсан диагонал дээр байгаа $a$ тэмээ гэсэн хосын тоог тоолъё. Тэмээ бүр өөрийн байгаа нүдийг оруулаад дор хаяж $n$ нүд идэх тул энэ тоо хамгийн багадаа $$A=(2n-2)\cdot n=2n^2-2n$$ байна. Нөгөө талаас өөр дээр нь тэмээ байрлаагүй булан биш нүд бүр яг хоёр тэмээнд, өөр дээр нь тэмээ байгаа нүд бүр яг нэг тэмээнд (өөртөө), тэмээгүй булангийн 2 нүд мөн адил яг нэг тэмээнд идүүлэх тул бидний сонирхож байгаа тоо яг $$B=2(n^2-4-(2n-4))+2n-2+2=2n^2-2n$$ байна. $A\le B$ ба тэнцэл биелэхийн тулд тэмээ бүр өөрийн нүдийг оруулаад яг $n$ тэмээ иддэг байх ёстой. Иймд бүх тэмээ захын нүдэнд байрлах шаардлагатай.
Одоо хүснэгтийн аль нэг тал дээр байрласан тэмээнүүд хөрш тал дээрх тэмээнүүдийг нэг утгатай тодорхойлдог гэдгийг харуулъя. Хөрш талуудын нүд бүр нөгөө талынхаа яг нэг нүдтэй тэмээний нүүдлээр холбогдоно. Диагонал бүр дээр яг нэг тэмээ байрлах ёстой тул эдгээрийн яг нэг дээр нь тэмээ байна. Эндээс аль ч тал нь нөгөө талуудаа нэг утгатай тодорхойлох нь харагдаж байна.
Аль нэг тал дээр нь дураараа тэмээ байрлуулаад өмнөх алхамд тодорхойлсон ёсоор хөрш болон бусад талуудыг нь тодорхойлбол бие биеэнээ идэхгүй $2n-2$ тэмээ байрлана. Нөгөө талаас аль нэг тал дээр нь тэмээ байрлуулах боломжийн тоо $2^n$ тул нийт боломжийн тоо мөн адил $2^n$ байна.
Одоо бүх тэмээ хүснэгтийн захын нүдэнд (хамгийн цөөн нүүдэлтэй нүднүүд) байрлах ёстойг харуулъя. $x$ нүд ба $x$ нүдийг агуулсан диагонал дээр байгаа $a$ тэмээ гэсэн хосын тоог тоолъё. Тэмээ бүр өөрийн байгаа нүдийг оруулаад дор хаяж $n$ нүд идэх тул энэ тоо хамгийн багадаа $$A=(2n-2)\cdot n=2n^2-2n$$ байна. Нөгөө талаас өөр дээр нь тэмээ байрлаагүй булан биш нүд бүр яг хоёр тэмээнд, өөр дээр нь тэмээ байгаа нүд бүр яг нэг тэмээнд (өөртөө), тэмээгүй булангийн 2 нүд мөн адил яг нэг тэмээнд идүүлэх тул бидний сонирхож байгаа тоо яг $$B=2(n^2-4-(2n-4))+2n-2+2=2n^2-2n$$ байна. $A\le B$ ба тэнцэл биелэхийн тулд тэмээ бүр өөрийн нүдийг оруулаад яг $n$ тэмээ иддэг байх ёстой. Иймд бүх тэмээ захын нүдэнд байрлах шаардлагатай.
Одоо хүснэгтийн аль нэг тал дээр байрласан тэмээнүүд хөрш тал дээрх тэмээнүүдийг нэг утгатай тодорхойлдог гэдгийг харуулъя. Хөрш талуудын нүд бүр нөгөө талынхаа яг нэг нүдтэй тэмээний нүүдлээр холбогдоно. Диагонал бүр дээр яг нэг тэмээ байрлах ёстой тул эдгээрийн яг нэг дээр нь тэмээ байна. Эндээс аль ч тал нь нөгөө талуудаа нэг утгатай тодорхойлох нь харагдаж байна.
Аль нэг тал дээр нь дураараа тэмээ байрлуулаад өмнөх алхамд тодорхойлсон ёсоор хөрш болон бусад талуудыг нь тодорхойлбол бие биеэнээ идэхгүй $2n-2$ тэмээ байрлана. Нөгөө талаас аль нэг тал дээр нь тэмээ байрлуулах боломжийн тоо $2^n$ тул нийт боломжийн тоо мөн адил $2^n$ байна.
3. Хурц өнцөгт, элдэв талт $ABC$ гурвалжин өгөгдөв. Уг гурвалжны дотор $A_1$ цэгийг $\measuredangle A_1AB=\measuredangle A_1BC$ ба $\measuredangle A_1AC=\measuredangle A_1CB$ байхаар авав. Үүнтэй адилаар $B_1$, $C_1$ цэгүүдийг тодорхойлсон бөгөөд уг гурвалжны орто төвийг $H$, хүндийн төвийг $G$ гэвэл $A_1$, $B_1$, $C_1$, $G$, $H$ цэгүүд нэг тойрог дээр оршино гэж батал.
Заавар Бодолт
Заавар. $A_1$, $B_1$, $C_1$ цэгүүд $GH$ диаметртэй тойрог дээр оршино гэж харуул.
Бодолт. Т. Хулан багшийн бодолт.
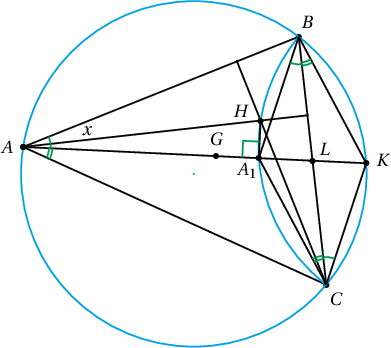 $AA_1$ нь багтаасан тойрогтой $K$ цэгт огтлолцдог байг. $\measuredangle A_1CB=\measuredangle KAC=\measuredangle KBC$ тул $AB\parallel KC$, $BK\parallel AC$ буюу $ABKC$ нь параллелограмм болно. Эндээс $AK\cap BC=L$ гэвэл $BL=LC$. Өөрөөр хэлбэл $A_1$ цэг нь $A$ оройн медиан дээр оршино. Энэ нум дээр мөн $H$ орто төв оршино. Иймд $B$, $C$, $A_1$, $H$ цэгүүд нэг тойрог дээр оршино.
$AA_1$ нь багтаасан тойрогтой $K$ цэгт огтлолцдог байг. $\measuredangle A_1CB=\measuredangle KAC=\measuredangle KBC$ тул $AB\parallel KC$, $BK\parallel AC$ буюу $ABKC$ нь параллелограмм болно. Эндээс $AK\cap BC=L$ гэвэл $BL=LC$. Өөрөөр хэлбэл $A_1$ цэг нь $A$ оройн медиан дээр оршино. Энэ нум дээр мөн $H$ орто төв оршино. Иймд $B$, $C$, $A_1$, $H$ цэгүүд нэг тойрог дээр оршино.
$\measuredangle ABC=\beta$, $\measuredangle BAK=x$ гэе. $\measuredangle ABA_1=\beta-x$. Иймд $$\measuredangle BA_1K=x+\measuredangle ABA_1=x+(\beta-x)=\beta$$ $\measuredangle HA_1B=\measuredangle HCB=90^\circ-\beta$. Эндээс $$\measuredangle HA_1K=\measuredangle HA_1B+\measuredangle BA_1K=(90^\circ-\beta)+\beta=90^\circ$$ Иймд $A_1$ нь $GH$ диаметртэй тойрог дээр оршино. Яг ижил шалтгаанаар $B_1$, $C_1$ цэгүүд энэ тойрог дээр оршино.

$\measuredangle ABC=\beta$, $\measuredangle BAK=x$ гэе. $\measuredangle ABA_1=\beta-x$. Иймд $$\measuredangle BA_1K=x+\measuredangle ABA_1=x+(\beta-x)=\beta$$ $\measuredangle HA_1B=\measuredangle HCB=90^\circ-\beta$. Эндээс $$\measuredangle HA_1K=\measuredangle HA_1B+\measuredangle BA_1K=(90^\circ-\beta)+\beta=90^\circ$$ Иймд $A_1$ нь $GH$ диаметртэй тойрог дээр оршино. Яг ижил шалтгаанаар $B_1$, $C_1$ цэгүүд энэ тойрог дээр оршино.
4. $\forall x\in\mathbb R$ хувьд $f(x+1)=f(x)+1$, $\forall x\in\mathbb R\setminus\{O\}$ хувьд $f(x)=x^2f\left(\frac{1}{x}\right)$ байх бүх сондгой $f\colon\mathbb R\to\mathbb R$ функцийг ол.
Заавар Бодолт
Заавар. Өгсөн нөхцөлүүд болон $f(x-1)=f(x)-1$-ийг ашиглан $f(x)$-ийг хувирга.
Бодолт. Т. Базарын ирүүлсэн бодолт.
$x\neq0$ ба $x\neq1$ бол \begin{align*} f(x)&=x^2\cdot f\left(\dfrac1x\right)=x^2\cdot f\left(1+\dfrac{1-x}{x}\right)\\ &=x^2+x^2\cdot f\left(\dfrac{1-x}{x}\right)\\ &=x^2+x^2\cdot \dfrac{(1-x)^2}{x^2}\cdot f\left(\dfrac{x}{1-x}\right)\\ &=x^2+(1-x)^2\cdot f\left(\dfrac{1}{1-x}-1\right)\\ &=x^2+(1-x)^2f\left(\dfrac{1}{1-x}\right)-(1-x)^2\\ &=x^2-(1-x)^2+f(1-x)\\ &=2x+f(-x)=2x-f(x) \end{align*} тул $f(x)=x$ болов. $f(2)=f(1)+1=2\Rightarrow f(1)=1$, $f(1)=f(0)+1=1\Rightarrow f(0)=0$ байна.
$x\neq0$ ба $x\neq1$ бол \begin{align*} f(x)&=x^2\cdot f\left(\dfrac1x\right)=x^2\cdot f\left(1+\dfrac{1-x}{x}\right)\\ &=x^2+x^2\cdot f\left(\dfrac{1-x}{x}\right)\\ &=x^2+x^2\cdot \dfrac{(1-x)^2}{x^2}\cdot f\left(\dfrac{x}{1-x}\right)\\ &=x^2+(1-x)^2\cdot f\left(\dfrac{1}{1-x}-1\right)\\ &=x^2+(1-x)^2f\left(\dfrac{1}{1-x}\right)-(1-x)^2\\ &=x^2-(1-x)^2+f(1-x)\\ &=2x+f(-x)=2x-f(x) \end{align*} тул $f(x)=x$ болов. $f(2)=f(1)+1=2\Rightarrow f(1)=1$, $f(1)=f(0)+1=1\Rightarrow f(0)=0$ байна.