Заавар. $K=MN\cap BD$ гээд $\triangle BKN$, $\triangle DKN$ гурвалжнууд адил хажуут гэдгийг харуул.

Бодолт. Т. Базарын ирүүлсэн бодолт: 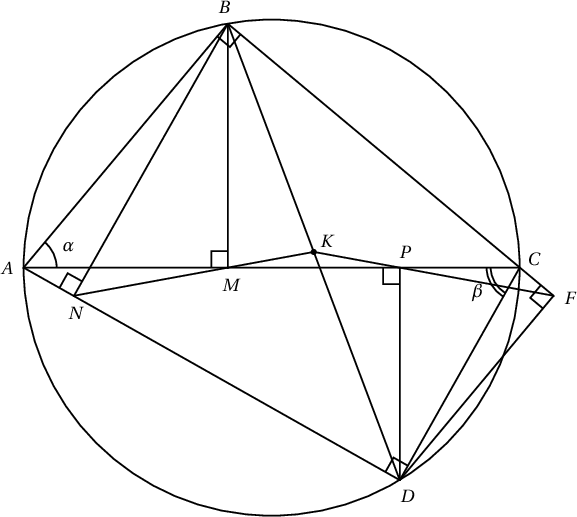$\angle BAC=\alpha$ гэе. $ANMB$ тойрогт багтсан тул $\angle BNM=\alpha$ байна. $\angle B=90^\circ$ тул $\angle BCA=90^\circ-\alpha$ ба $ABCD$ тойрогт багтсан тул $\angle BDA=\angle BCA=90^\circ-\alpha$ болно. Түүнчлэн $\triangle BND$ тэгш өнцөгт тул $$\angle NBD=90^\circ-(90^\circ-\alpha)=\alpha=\angle BNK$$ тул $BKN$ гурвалжин адил хажуут байна байна. Иймд $BK=KN$ байна. Түүнчлэн $\triangle BND$ тэгш өнцөгт гурвалжин тул $K$ цэг гипотенузын дундаж цэг болно. Нөгөө талаас яг адил шалтгаанаар $PF\cap BD$ нь $BD$ хэрчмийн дундаж цэг буюу $K$ болно.

Үнэндээ $PCFD$ тойрогт багтсан тул $\beta=\angle PCD=\angle PFD$, $ABCD$ тойрогт багтсан ба $\angle ADC=90^\circ$ тул $$\angle CDB=\angle CAD=90^\circ-\beta$$ ба $\angle BFP=90^\circ-\beta$ тул $\triangle BKF$ мөн адил хажуут гурвалжин болно.

Заавар. $c\mid ab$ ба $(a,c)=1$ бол $c\mid b$ байдаг.

Бодолт. Х. Санжаахүүгийн бодолт:

$x=\dfrac{p}{q}$, $(p,q)=1$ ба $(pm,qn)=d$ гэе. Тэгвэл $$f\left(\dfrac{m}{n}x\right)=\dfrac{pm}{d}+\dfrac{qn}{d}=\dfrac{pm+qn}{d}$$ ба $f(x)=f\left(\dfrac{m}{n}x\right)$ тул $$f(x)=p+q=\dfrac{pm+qn}{d}$$ Иймд $p+q\mid pm+qn=q(n-m)+m(p+q)\Rightarrow p+q\mid q(n-m)$ болно. Түүнчлэн $(p+q,q)=1$ тул $p+q\mid m-n$ болж батлах зүйл батлагдав.

Заавар. $n=2^k$ үед бодлого үнэн гэдгийг батлаад дараа нь $n=m$ үед үнэн гэдгээ ашиглан $n=m-1$ үед үнэн болохыг харуул.

Бодолт. $n=m$ үед үнэн бол $n=2m$ үед ч үнэн болохыг баталъя. \begin{align*} f(x_1x_2\cdots x_{2m})&=\dfrac{f\big((x_1x_2\cdots x_m)^2\big)+f\big((x_{m+1}x_{m+2}\cdots x_{2m})^2\big)}{2}\\ &=\dfrac{f(x_1^2x_2^2\cdots x_m^2)+f(x_{m+1}^2x_{m+2}^2\cdots x_{2m}^2)}{2}\\ &=\dfrac{\dfrac{f((x_1^2)^{m})+\cdots+f((x_m^2)^{m})}{m}+\dfrac{f((x_{m+1}^{2})^m)+\cdots+f((x_{2m}^2)^m)}{m}}{2}\\ &=\dfrac{f(x_1^{2m})+f(x_2^{2m})+\cdots+f(x_{2m}^{2m})}{2m} \end{align*} болно. Иймд индукцээр $n=2^k$ үед үнэн байна. Одоо $n=m$ үед үнэн бол $n=m-1$ үед үнэн болохыг харуулъя.

$z_1=x_1^{\frac{m-1}{m}}$, $z_2=x_2^{\frac{m-1}{m}},\cdots, z_{m-1}=x_{m-1}^{\frac{m-1}{m}}$, $z_m=z_1\cdots z_{m-1}$ тоонуудын хувьд \begin{align*} f(x_1x_2\cdots x_{m-1})&=f(z_1z_2\cdots z_m)\\ &=\dfrac{f(z_1^m)+f(z_2^m)+\cdots+f(z_{m}^m)}{m}\\ &=\dfrac{f(x_1^{m-1})+\cdots+f(x_{m-1}^{m-1})+f(x_1x_2\cdots x_{m-1})}{m} \end{align*} тул $$f(x_1x_2\cdots x_{m-1})=\dfrac{f(x_1^{m-1})+\cdots+f(x_{m-1}^{m-1})}{m-1}$$ байна. Ямар ч $n$ натурал тооноос их $2^k$ хэлбэрийн тоо оршин байх тул $$\dfrac{\sum_{i=1}^nf(x_i^n)}{n}=f(x_1x_2x_3\cdots x_n)$$ болох нь батлагдав.

Дээрх баталгааны арга нь Кошийн тэнцэтгэл бишийг индукцээр батлахад ашигладаг санаа гэдгийг уншигч та бүхэн андахгүй биз. Энэ аргаар бодох санааг өгсөн Т. Базартаа талархал илэрхийлье.

Заавар. $n\times n$ хүснэгтийн хувьд хамгийн олондоо хэдэн даам байрлуулж болох вэ? $n$-ийн бага утгуудыг ашиглан үнэлгээ хий.

Бодолт. $n=5$ үед гэсэн 12 даамтай байгуулалтууд байж болж байна. 13 даам байрлуулж болохгүйг харуулахад төвөгтэй биш.

$n=10$ үед хамгийн олондоо 34 даам байж болохыг харуулъя. Мөр ба багануудын байрыг солиход параллел талуудтай тэгш өнцөгт үүсэхгүй. Иймд ямар нэг мөрөнд 5 даам байрладаг бол түүнийг 1-р мөр, даамнууд нь эхний баганууд дээр байрладаг гэж үзэж болно. $A$ хүснэгтийн аль ч мөрөнд 2 даам байрлаж болохгүй тул хамгийн олондоо 9 даамтай. $B$ хүснэгтийн багана бүр 4-өөс цөөн даамтай гэвэл хамгийн олондоо 15 даамтай буюу нийт даамны тоо $5+9+15=29$-өөс хэтрэхгүй. Аль нэг баганад 4 даам байрладаг гэвэл дараах хэлбэртэй гэж үзэж болно. $C$ хүснэгтийн багана бүрд 2-оос цөөн даам байрлах тул хамгийн олондоо 4 даам байрлана. $D$ хүснэгт нь $5\times 5$ тул хамгийн олондоо $12$ даам байрлана. Иймд нийт даамны тоо $5+9+4+4+12=34$-өөс хэтрэхгүй.

Аль нэг мөрөнд 6, 7, 8, 9 даам байрлах тохиолдолд дээрхтэй адил аргаар $34$-өөс хэтрэхгүй даам байрлуулж болохыг баталж болно. Үүнийг та бүхэнд үлдээгээд аль ч мөр ба баганад 4-өөс хэтрэхгүй даам байх тохиолдолд дээр өгүүлбэрийг батлаад даамнууд хүснэгтийн талтай параллел талуудтай тэгш өнцөгт үүсгэхгүй байхаар 34 даам байрлуулж болохыг жишээгээр харуулъя.

Аль ч мөр ба баганад 4-өөс олон даам байрладаггүй гэе. Тэгвэл мөр ба багануудын байрыг солих замаар дараах дүрсийг гаргаж болно. Эсрэг тохиолдолд 5, 6, 7, 8, 9, 10-р баганад тус бүр 3-аас хэтрэхгүй даам буюу нийт 18 даам байрлах ба $A$ дүрсэд хамгийн олондоо 9 даам байрлах тул нийт даамны тоо $4+9+6\cdot 3=31$-аас хэтрэхгүй. Зурагт байгаа $A$ дүрсэд хамгийн олондоо 9 даам, $B$ дүрсэд хамгийн олондоо 5 даам, $C$ нь $5\times5$ хүснэгт тул $C$ дүрсэд хамгийн олондоо 12 даам байна. Түүнчлэн мөр ба багана бүрд 4-өөс олонгүй даам байрлах ёстой тул бусад нүднүүдэд даам байрлахгүй. Иймд даамны тоо хамгийн олондоо $4+4+9+5+12=34$ байна.

34 даам байрлах жишээ нь: