Бүсийн олимпиад 2018, 10-р анги
Бодлогын тоо: 4 Хугацаа: 180 мин
1. $a+b=2018$ бөгөөд $x^2+ax+b=0$ тэгшитгэл нь бүхэл шийдтэй байдаг бүх бүхэл $a$, $b$ тоонуудыг ол.
Заавар Бодолт
Заавар.
Бодолт. Бүхэл шийдүүд нь $m$, $n$ гэе. Тэгвэл Виетийн теоремоор
$$m+n=-a, mn=b\Rightarrow mn-m-n=a+b=2018$$
болно. Иймд
$$(m-1)(n-1)=2019$$
Эндээс $m$, $n$ нь тэгш эрхтэй тул
$$\left\{\begin{array}{c}
m-1=-1\\
n-1=-2019
\end{array}\right.\lor
\left\{\begin{array}{c}
m-1=-3\\
n-1=-673
\end{array}\right.\lor
\left\{\begin{array}{c}
m-1=1\\
n-1=2019
\end{array}\right.\lor
\left\{\begin{array}{c}
m-1=3\\
n-1=673
\end{array}\right.
$$
буюу
$$\left\{\begin{array}{c}
m=0\\
n=-2018
\end{array}\right.\lor
\left\{\begin{array}{c}
m=-2\\
n=-672
\end{array}\right.\lor
\left\{\begin{array}{c}
m=2\\
n=2020
\end{array}\right.\lor
\left\{\begin{array}{c}
m=4\\
n=674
\end{array}\right.
$$
гэж үзэж болно. Иймд $(a,b)$ нь $(2018,0)$; $(674,1344)$; $(-2022,4040)$; $(-678,2696)$ байна.
2. Зөв $ABC$ гурвалжны гадна талд $ABDE$ квадратыг байгуулжээ (зураг). $AD$, $CE$ хэрчмүүд $K$ цэгт огтлолцдог бол $CK=DK$ гэдгийг батал.
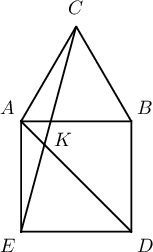
Заавар Бодолт
Заавар. $\measuredangle KCD=\measuredangle KDC$ гэж батал.
Бодолт. $\angle CAE=90^\circ+60^\circ=150^\circ$, $AC=AE$ тул
$$\measuredangle ACE=\measuredangle AEC=\dfrac{180^\circ-150^\circ}{2}=15^\circ$$
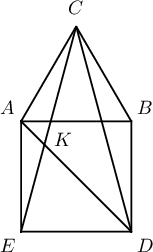$\triangle ACE=\triangle BCD$ тул $\measuredangle BCD=\measuredangle BDC=15^\circ$ байна.
$$\measuredangle KCD=60^\circ-2\cdot 15^\circ=30^\circ,$$
$$\measuredangle KDC=45^\circ-15^\circ=30^\circ$$
буюу $\measuredangle KCD=\measuredangle KDC$ тул $\triangle KCD$ гурвалжин адил хажуут гурвалжин болно. Иймд $CK=DK$ байна.
3. $10\times10$ хэмжээтэй хөлгийн нүднүүдэд $1$-ээс $100$ хүртэл тоонуудыг ямар нэг дарааллаар бичжээ. Дотор нь бичигдсэн гурван тооны нийлбэр нь $3$-д хуваагддаг $3$ нүдтэй булан дүрс олдохыг батал.
Заавар Бодолт
Заавар.
Бодолт. Эсрэгээр нь дээр нь бичигдсэн 3 тооны нийлбэр нь 3-д хувааддаг булан дүрс олддоггүй гэе. Бичигдсэн тоонуудынхаа оронд тухайн тоог 3-д хуваахад гарах үлдэгдлүүдийг авч үзье. Аливаа булан дүрсэд бичигдсэн 3 тооны нийлбэр 3-д хуваагдахгүй тул үлдэгдлүүд нь бүгд ялгаатай байж болохгүй. Иймд аль ч булан дүрсэд 3-д хуваахад ижил үлдэгдэл өгдөг 2 тоо олдоно. Түүнчлэн аливаа $2\times 2$ дүрсэд 3-д хуваахад ижил үлдэгдэл өгөх 3 тоо байхгүй тул тоонуудыг нь 2, 2-оор нь 3-д хуваахад ижил үлдэгдэл өгдөг байхаар бүлэглэж болно. Эндээс хүснэгтэд бичигдсэн тоонууд дотор 3-д хуваагдах тоо тэгш тоотой болоход хүрч байна. Гэтэл 1-ээс 100 хүртэлх тоонууд дотор 33 ширхэг 3-д хуваагдах тоо байх тул зөрчил үүсэв. Иймд аль нэг булан дүрсэд бичигдсэн тоонуудын нийлбэр 3-д хуваагдана.
4. $a$, $b$, $c$ нь $abc=1$ байх эерэг тоонууд бол
$$\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{9}{2(a+b+c)}\ge\dfrac92$$
тэнцэтгэл биш биелэхийг батал.
Заавар Бодолт
Заавар. Т. Базарын ирүүлсэн бодолт.
$\forall x,y,z\in\mathbb R$ тоонуудын хувьд $$\dfrac{(x+y+z)^2}{3}\ge xy+yz+zx$$ болохыг ашигла. Тэнцэтгэл биш $x=y=z$ үед тэнцэлдээ хүрнэ. Үнэндээ $$\dfrac{(x+y+z)^2}{3}\ge xy+yz+zx\Leftrightarrow x^2+y^2+z^2-xy-yz-zx\ge 0$$ ба сүүлийн тэнцэтгэл биш нь $(x-y)^2+(y-z)^2+(z-x)^2\ge$ илт тэнцэтгэл бишээс мөрдөн гарна.
$\forall x,y,z\in\mathbb R$ тоонуудын хувьд $$\dfrac{(x+y+z)^2}{3}\ge xy+yz+zx$$ болохыг ашигла. Тэнцэтгэл биш $x=y=z$ үед тэнцэлдээ хүрнэ. Үнэндээ $$\dfrac{(x+y+z)^2}{3}\ge xy+yz+zx\Leftrightarrow x^2+y^2+z^2-xy-yz-zx\ge 0$$ ба сүүлийн тэнцэтгэл биш нь $(x-y)^2+(y-z)^2+(z-x)^2\ge$ илт тэнцэтгэл бишээс мөрдөн гарна.
Бодолт. \begin{align*}
a+b+c&=abc(a+b+c)\\
&=(ab)\cdot(ac)+(ab)\cdot(bc)+(ac)\cdot(bc)\\
&\le\dfrac{(ab+bc+ca)^3}{3} & (*)
\end{align*}
болно. $\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=ab+bc+ca$ тул
\begin{align*}
\text{ЗГТ}&=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{9}{2(a+b+c)}\\
&\overset{(*)}{\ge} ab+bc+ca+\dfrac{27}{2(ab+bc+ca)^2}\\
&=\dfrac{ab+bc+ca}{2}+\dfrac{ab+bc+ca}{2}+\dfrac{27}{2(ab+bc+ca)^2}\\
&\kern-0.5em\overset{\text{Коши}}{\ge}3\sqrt[3]{\dfrac{27}{8}}=\dfrac{9}{2}
\end{align*}
болж батлагдав. Тэнцэтгэл биш $a=b=c=1$ үед тэнцэлдээ хүрнэ.