Заавар. Энэ тоо нь 9-д хуваагдах тоо ба 9-д хуваахад 8 үлдэгдэл өгдөг хуваагчтай байна.

Бодолт. $9$ ба $9$-д хуваахад 8 үлдэгдэл өгдөг тоонууд нь харилцан анхны байна. Иймд $9\cdot (9k+8)\cdot s$ хэлбэртэй тоонууд дотроос $n$-ийг хайж олно. $k=0$ байх шийдийг хайвал $s=4$ үед $n=2^5\cdot 3^2=288$ тооны хуваагчдын цифрүүдийн нийлбэр $S(1)=1$, $S(2)=2$, $S(3)=3$, $S(4)=4$, $S(32)=5$, $S(6)=6$, $S(16)=7$, $S(8)=8$, $S(9)=9$ байна.$k\ge 3$ үед $9\cdot(9k+8)>288$ тул хамгийн бага шийд олдохгүй.

$k=1$ үед $n=9\cdot 17\cdot s=153s$ ба $s\ge 2$ үед $153s>288$ тул $s=1$ тохиолдлыг шалгая. Энэ тохиолдолд $n=3^2\cdot 17$ нь 6 хуваагчтай тул бодлогын шийд болохгүй.

$k=2$ үед $n=9\cdot 26\cdot s$ тул мөн адил $s=1$ тохиолдлыг шалгахад хангалттай. $n=2\cdot 3^2\cdot 13=234$ тоо нь $$1,2,3,6,9,13,18,26,39,78,117,234$$ гэсэн $12$ ширхэг хуваагчтай. Эдгээр дунд цифрүүдийн нийлбэр нь 5-тай тэнцүү байхгүй тул бодлогын шийд болохгүй. Иймд бодлогын нөхцөлийг хангах хамгийн бага натурал тоо бол $288$ юм.

Заавар. Нэг мөр, эсвэл багана будагдаагүй үлдэх тул 8 нүдтэй тэгш өнцөгт ямагт олдоно. $3\times3$, $2\times 5$ тэгш өнцөгтүүд үргэлж олдох албатай юу?

Бодолт. 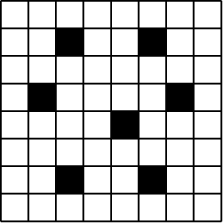гэж будахад $3\times 3$, $2\times 5$ хэмжээтэй огт будагдаагүй тэгш өнцөгт олдохгүй. Нөгөө талаас $8\times8$ хүснэгтийн $8$-аас олон нүдтэй дэд хүснэгт бүр дээрх хоёр хүснэгтийн аль нэгийг нь заавал дотроо агуулна. Иймд бодлогын хариу $8$ байна.

Заавар. $2$ тоо заавал нэг хэсэгт орох тоонуудыг ол.

Бодолт. $2$-д хуваагддаг бүх тоонууд $2$-той нэг хэсэгт орох ёстой. Иймд $2\cdot 3$, $2\cdot 5$, $2\cdot 7$, $2\cdot 11$, $2\cdot 13$, $2\cdot 17$, $2\cdot 19$, $2\cdot 23$ тоонууд $2$-той нэг хэсэгт орно. Эндээс $3$, $5$, $7$, $11$, $13$, $17$, $19$, $23$ гэсэн $25$-аас бага бүх анхны тоонд хуваагддаг тоонууд $2$-той нэг хэсэгт орох болов. Эдгээр нь $25$-аас их анхны тоонууд буюу $29$, $31$, $37$, $41$, $43$, $47$ ба $1$ юм. Учир нь эдгээрээс бусад бүх зохиомол тоонд $7$-оос хэтрэхгүй анхны тоон хуваагч бий. Эдгээр $7$ тоонууд нь $2$-той нэг хэсэгт орсон, ороогүй байхаар хуваах ялгаатай аргын тоо нь $2^7-1=127$ (бүх тоо нэг хэсэгт байж болохгүй) эдгээр хуваалтын хувьд хэсэг тус бүрд байгаа тоонуудын үржвэр нь харилцан анхны байна. Иймд $127$ ялгаатай аргаар хувааж болно.

Заавар. Бууз захиалаад бууз идэж байгаа хүний дундаж тоог бод.

Бодолт. Бууз захиалсан хүнийг хөх цэгээр, хуушуур захиалсан хүнийг улаан цэгээр тэмдэглэе. Дараах тохиолдолд хамгийн олондоо 10 хүнд захиалсан хоолыг нь өгөх боломжтой. 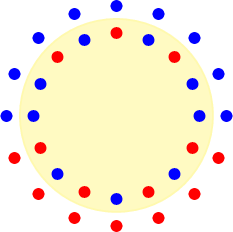Одоо ямар ч тохиолдолд нэг эргүүлээд 10 хүнд захиалсан хоолыг өгөх боломжтой гэдгийг харуулъя. Ширээг 16 удаа тойруулж эргүүлэхэд бууз захиалсан хүн бүр яг 9 удаа буузтай таарна. Эдгээрийн нийт тоо нь $9\cdot 9=81$ болох бөгөөд эдгээрийг 16 тохиолдолд дундачилбал $\dfrac{81}{16}>5$ болно. Иймд аль нэг эргэлтэнд дор хаяж 6 хүн бууз идэх ёстой. Энэ тохиолдолд бууз идээгүй 3 хүн л хуушуур идэх тул дор хаяж 4 ширхэг хуушуур захиалсан хүн хуушуур иднэ. Иймд нийт 10 хүн захиалсан хоолоо иднэ.