Энхболд XV, 8-р анги
Бодлогын тоо: 4 Хугацаа: 180 мин
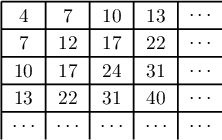
1. Зурагт үзүүлсэн хүснэгтийн эхний мөр, баганын тоонууд 3-аар өснө, 2-р мөр, баганын тоонууд 5-аар өснө, 3-р мөр баганын тоонууд 7-оор өснө, гэх мэтчилэн үргэлжилнэ. Энэ төгсгөлгүй хүснэгтэд бичигдсэн ямар ч $n$ тооны хувьд $2n+1$ нь зохиомол тоо гэдгийг батал.

Заавар Бодолт
Заавар. $i$-р мөр $j$-р баганын огтлолцолд ямар тоо бичигдэхийг $i$, $j$-ээр илэрхийл.
Бодолт. $1$-р мөрний $j$-р тоо $1+3j$ байна. $j$-р баганын тоонууд нь $2j+1$-ээр ихэснэ. Иймд энэ баганын $i$-р мөрөнд
$$1+3j+(i-1)(2j+1)=2ij+i+j$$
тоо бичигдэнэ. Нөгөө талаас
$$2(2ij+i+j)+1=4ij+2i+2j+1=(2i+1)(2j+1)$$
тоо зохиомол тоо юм.
2. 4-өөс олон хуваагчтай натурал $n$ тооны бүх хуваагчдыг өсөх эрэмбээр $a < b < c < d <\dots$ гэж эрэмбэлжээ. $n=a^2+b^2+c^2+d^2$ байх бүх $n$ тоог ол.
Заавар Бодолт
Заавар. $n$ тэгш тоо болохыг харуул.
Бодолт. 1-р сургуулийн 11-р ангийн сурагч Маралгүний бодолт:
$n$ сондгой тоо гэвэл хуваагч бүр нь сондгой болно. Нөгөө талаас дөрвөн ширхэг сондгой хуваагчийн квадратуудын нийлбэр нь тэгш тоо гарах тул $n$ тоо тэгш болоход хүрч зөрчил үүснэ. Иймд $n=2n'$ байна.
Иймд $1^2+2^2+c^2+d^2=2n'$ болно.
$c$ сондгой бол $d$ тэгш тоо байх шаардлагатай. Энэ тохиолдолд $d=2c$ байна. Эндээс $n=5(1+c^2)$ тул $c=3\lor 5$ байна. $c=3$ бол $n=50$ ба $$50\neq 1^2+2^3+3^2+5^2$$ тул шийд болохгүй. $c=5$ бол $n=130$ ба $$130=1^2+2^2+5^2+10^2$$ тул шийд болно.
$c$ тэгш тоо бол $d$ сондгой тоо байх шаардлагатай ба $c=4$ байна. Иймд $n=4n''$ байна. Гэтэл сондгой тооны квадрат 4-д 1 үлдэгдэл өгөх тул $$1^2+2^2+4^2+d^2\equiv 2\not\equiv 0\pmod{4}$$ болж зөрчил үүсэв.
Иймд бодлогын нөхцөлийг хангах тоо нь зөвхөн $n=130$ байна.
$n$ сондгой тоо гэвэл хуваагч бүр нь сондгой болно. Нөгөө талаас дөрвөн ширхэг сондгой хуваагчийн квадратуудын нийлбэр нь тэгш тоо гарах тул $n$ тоо тэгш болоход хүрч зөрчил үүснэ. Иймд $n=2n'$ байна.
Иймд $1^2+2^2+c^2+d^2=2n'$ болно.
$c$ сондгой бол $d$ тэгш тоо байх шаардлагатай. Энэ тохиолдолд $d=2c$ байна. Эндээс $n=5(1+c^2)$ тул $c=3\lor 5$ байна. $c=3$ бол $n=50$ ба $$50\neq 1^2+2^3+3^2+5^2$$ тул шийд болохгүй. $c=5$ бол $n=130$ ба $$130=1^2+2^2+5^2+10^2$$ тул шийд болно.
$c$ тэгш тоо бол $d$ сондгой тоо байх шаардлагатай ба $c=4$ байна. Иймд $n=4n''$ байна. Гэтэл сондгой тооны квадрат 4-д 1 үлдэгдэл өгөх тул $$1^2+2^2+4^2+d^2\equiv 2\not\equiv 0\pmod{4}$$ болж зөрчил үүсэв.
Иймд бодлогын нөхцөлийг хангах тоо нь зөвхөн $n=130$ байна.
3. Өвлийн өвгөн хэдэн уутанд 1 г, 2 г, $\ldots$, 24 г, 25 г жинтэй чихрээс 100, 100 ширхэг чихэр хийхэд бүх уутны жин ялгаатай болсон байв. Цасан охин уут тус бүрээс хамгийн хүнд 1 чихэр, хамгийн хөнгөн 1 чихрийг аваад идчихжээ. Тэгэхэд аль ч 2 уутны өмнө хүнд байсан уут нь одоо хөнгөн болсон байв. Хамгийн олондоо хэдэн уут чихэр байсан бэ?
Заавар Бодолт
Заавар. Бодлогын нөхцөлийг хадгалж байхаар ууттай чихэрүүдийг хэрхэн өөрчилж болох вэ? Бодлогын нөхцөлөөс уут бүр дэх хүнд хөнгөн чихрүүдийн жингийн нийлбэр нь дор хаяж 2-оор зөрөөтэй байна гэж гарна.
Бодолт. Уут бүрд 1 г эсвэл 25 г жинтэй чихэр байгаа тохиолдолд хамгийн олондоо хэдэн уут чихэр байж болохыг олоход хангалттай. Эсрэг тохиолдолд хамгийн бага жинтэйг нь 1 граммаар багасгаад, хамгийн их жинтэйг нь 1 граммаар ихэсгэхэд бодлогын нөхцөл хадгалагдах ба энэ үйлдлээ давтаад уут бүрийг 1 г эсвэл 25 г жинтэй чихэртэй болгож болно.
А уут Б уутнаас хүнд байсан байг. Иймд А уутнаас авсан чихрүүдийн жин Б уутнаас авсан чихрүүдийн жингээс хүнд байх ёстой. Хэрвээ Б уутанд 25 г жинтэй чихэр байсан бол А уутанд мөн л 25 г жинтэй чихэр байх шаардлагатай. Эсрэг тохиолдолд А уутанд 1 г жинтэй чихэр байх ёстой бөгөөд А уутнаас авсан 2 чихэр 25-аас их жинтэй байж чадахгүй. Гэтэл Б уутнаас дор хаяж 26 гр жинтэй чихэр авна.
Иймд хамгийн хөнгөн уутнуудад 1 г жинтэй чихрүүд, хамгийн хүнд жинтэй уутнуудад 25 г жинтэй чихэр бий гэж үзэж болно. 1 г жинтэй чихэртэй хөнгөн уутнуудын хамгийн хүндүүдийг $a_1 < a_2 < \dots < a_k$, 25 г чихэртэй хүнд уутнуудын хамгийн хөнгөнүүдийг $b_1 < b_2 < \dots < b_s$ гэе. Тэгвэл $$1+a_1 \le 1+a_2-2 \le 1+a_3-2\cdot2 \le \cdots \le 1+a_s-2\cdot (s-1)$$ ба $$b_1+25 \le b_2+25-2 \le b_3+25-2\cdot 2 \le \cdots \le b_k+25-2\cdot(k-1)$$ байна. Түүнчлэн $$1+a_s \le b_1+25-2$$ тул $$\left\{\begin{array}{c} 1+a_1\le 1+a_s-2(s-1)\\ b_1+25\le b_k+25-2(k-1)\\ 1+a_s\le b_1+25-2 \end{array}\right.$$ болно. Тэнцэтгэл бишүүдийг нэмбэл $$1+a_1+b_1+25+1+a_s\le 1+a_s-2(s-1)+b_k+25-2(k-1)+b_1+25-2$$ $$\Leftrightarrow 2(s+k)\le 26+ b_k-a_1\le 26+25-1=50$$ тул $s+k\le 25$ буюу хамгийн ихдээ $25$ уут байх боломжтой.
А уут Б уутнаас хүнд байсан байг. Иймд А уутнаас авсан чихрүүдийн жин Б уутнаас авсан чихрүүдийн жингээс хүнд байх ёстой. Хэрвээ Б уутанд 25 г жинтэй чихэр байсан бол А уутанд мөн л 25 г жинтэй чихэр байх шаардлагатай. Эсрэг тохиолдолд А уутанд 1 г жинтэй чихэр байх ёстой бөгөөд А уутнаас авсан 2 чихэр 25-аас их жинтэй байж чадахгүй. Гэтэл Б уутнаас дор хаяж 26 гр жинтэй чихэр авна.
Иймд хамгийн хөнгөн уутнуудад 1 г жинтэй чихрүүд, хамгийн хүнд жинтэй уутнуудад 25 г жинтэй чихэр бий гэж үзэж болно. 1 г жинтэй чихэртэй хөнгөн уутнуудын хамгийн хүндүүдийг $a_1 < a_2 < \dots < a_k$, 25 г чихэртэй хүнд уутнуудын хамгийн хөнгөнүүдийг $b_1 < b_2 < \dots < b_s$ гэе. Тэгвэл $$1+a_1 \le 1+a_2-2 \le 1+a_3-2\cdot2 \le \cdots \le 1+a_s-2\cdot (s-1)$$ ба $$b_1+25 \le b_2+25-2 \le b_3+25-2\cdot 2 \le \cdots \le b_k+25-2\cdot(k-1)$$ байна. Түүнчлэн $$1+a_s \le b_1+25-2$$ тул $$\left\{\begin{array}{c} 1+a_1\le 1+a_s-2(s-1)\\ b_1+25\le b_k+25-2(k-1)\\ 1+a_s\le b_1+25-2 \end{array}\right.$$ болно. Тэнцэтгэл бишүүдийг нэмбэл $$1+a_1+b_1+25+1+a_s\le 1+a_s-2(s-1)+b_k+25-2(k-1)+b_1+25-2$$ $$\Leftrightarrow 2(s+k)\le 26+ b_k-a_1\le 26+25-1=50$$ тул $s+k\le 25$ буюу хамгийн ихдээ $25$ уут байх боломжтой.
4. Дараах 2 нөхцөл биелж байхаар бүх натурал тоог улаан, хөх 2 өнгөөр хэдэн ялгаатай аргаар будаж болох вэ?
- Ямар ч натурал $n$ тооны хувьд $n$ ба $n+20$ тоо нь ижил өнгөтэй,
- Ямар ч натурал $n$ тооны хувьд $n$ ба $n+18$ тоонуудын ядаж нэг нь улаан өнгөтэй.
Заавар Бодолт
Заавар. Хялбар бодлогуудад шилжүүлж бод.
Бодолт. $n$ ба $n+20$ нь ижил өнгөтэй тул 20 үетэй байна. Иймд зөвхөн эхний 20-тоог хэрхэн будсанаар бүх тоонуудын будалт тодорхой болно.
$n$ ба $n+20$ тоонууд ижил өнгөтэй, $n$ ба $n+18$-ийн ядаж нэг нь улаан өнгөтэй тул $n+20$ ба $n+18$ тоонуудын ядаж нэг нь улаан өнгөтэй байна. Эндээс дараалсан хоёр тэгш тоо ба дараалсан хоёр сондгой тооны ядаж нэг нь улаан өнгөтэй болно.
Бодлогын нөхцөлийг хангахаар будах тоо нь эхний 10 сондгой тоог дараалсан хоёр хөх цэг байхгүй байхаар 2 өнгөөр будаж тойрог дээр байрлуулах ба эхний 10 тэгш тоог дараалсан хоёр хөх цэг байхгүй байхаар 2 өнгөөр будаж тойрог дээр байрлуулах тоотой ижил юм.
$n$ цэгийг дараалсан хоёр хөх цэг байхгүй ба эхлэл төгсгөл нь ижилхэн хөх биш байхаар улаан ба хөх өнгөөр хэчнээн аргаар будаж болохыг тоолъё. Үүний тулд дараах хүснэгтийг ашиглая.
Хүснэгтийн эхний баганад эхлэл ба төгсгөлийн цэгийн өнгийг, эхний мөрөнд цэгийн тоог тэмдэглэсэн бөгөөд хүснэгтийн тоонууд нь тухайн эхлэл ба төгсгөлтэй дараалсан хоёр хөх цэг байхгүй байх будалтын тоог тэмдэглэсэн болно. Энэ тохиолдолд эхний мөрийн тоонууд нь өмнөх баганын 1 ба 2-р мөрийн тоонуудын нийлбэр, хоёр дахь мөрийн тоонууд нь өмнө баганын 1-р мөрийн тоо, 3 дахь мөрийн тоо нь өмнөх баганын 3 ба 4-р мөрийн тоонуудын нийлбэр, 4 дэх мөрийн тоо нь өмнөх баганын 3-р мөрийн тоотой тэнцүү байна.
Бид эхлэл ба төгсгөлийн өнгө нь хоёулаа хөх биш ба дараалсан хоёр хөх цэг байхгүй байхаар 10 цэгийг будах тоог сонирхож байгаа тул энэ тоо нь дээрх хүснэгтийн сүүлийн баганын эхний 3 тооны нийлбэр буюу $55+34+34=123$ байна.
Иймд бодлогын нөхцөлийг хангах будалтын тоо $123^2=15129$ байна.
$n$ ба $n+20$ тоонууд ижил өнгөтэй, $n$ ба $n+18$-ийн ядаж нэг нь улаан өнгөтэй тул $n+20$ ба $n+18$ тоонуудын ядаж нэг нь улаан өнгөтэй байна. Эндээс дараалсан хоёр тэгш тоо ба дараалсан хоёр сондгой тооны ядаж нэг нь улаан өнгөтэй болно.
Бодлогын нөхцөлийг хангахаар будах тоо нь эхний 10 сондгой тоог дараалсан хоёр хөх цэг байхгүй байхаар 2 өнгөөр будаж тойрог дээр байрлуулах ба эхний 10 тэгш тоог дараалсан хоёр хөх цэг байхгүй байхаар 2 өнгөөр будаж тойрог дээр байрлуулах тоотой ижил юм.
$n$ цэгийг дараалсан хоёр хөх цэг байхгүй ба эхлэл төгсгөл нь ижилхэн хөх биш байхаар улаан ба хөх өнгөөр хэчнээн аргаар будаж болохыг тоолъё. Үүний тулд дараах хүснэгтийг ашиглая.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| УУ | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
| УХ | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 |
| ХУ | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 |
| ХХ | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 |
Хүснэгтийн эхний баганад эхлэл ба төгсгөлийн цэгийн өнгийг, эхний мөрөнд цэгийн тоог тэмдэглэсэн бөгөөд хүснэгтийн тоонууд нь тухайн эхлэл ба төгсгөлтэй дараалсан хоёр хөх цэг байхгүй байх будалтын тоог тэмдэглэсэн болно. Энэ тохиолдолд эхний мөрийн тоонууд нь өмнөх баганын 1 ба 2-р мөрийн тоонуудын нийлбэр, хоёр дахь мөрийн тоонууд нь өмнө баганын 1-р мөрийн тоо, 3 дахь мөрийн тоо нь өмнөх баганын 3 ба 4-р мөрийн тоонуудын нийлбэр, 4 дэх мөрийн тоо нь өмнөх баганын 3-р мөрийн тоотой тэнцүү байна.
Бид эхлэл ба төгсгөлийн өнгө нь хоёулаа хөх биш ба дараалсан хоёр хөх цэг байхгүй байхаар 10 цэгийг будах тоог сонирхож байгаа тул энэ тоо нь дээрх хүснэгтийн сүүлийн баганын эхний 3 тооны нийлбэр буюу $55+34+34=123$ байна.
Иймд бодлогын нөхцөлийг хангах будалтын тоо $123^2=15129$ байна.