Сайн гараа 2018, 9-р анги
Бодлогын тоо: 4 Хугацаа: мин
1. Аливаа 9 тооных нь нийлбэр бүтэн квадрат болдог байх ялгаатай 10 бүхэл тоо оршин байх уу?
Заавар Бодолт
Заавар. $S=x_1+x_2+\cdots +x_{10}$ ба $S-x_i=a_i^2$ байхаар $x_i$, $a_i\in\mathbb N$ тоонуудыг олох ёстой.
Бодолт. $S-x_i=a_i^2$ илэрхийллүүдийг нэмбэл $10S-S=\sum a_i^2$ болно. Иймд $S=\dfrac{\sum a_i^2}{9}$ байна.
$a_i=3(k+i)$, $i\in[10]$ байхаар сонговол \begin{align*} S&=\sum\limits_{i=1}^{10} (k+i)^2=\sum_{i=1}^{10}(k^2+2ki+i^2)\\ &=10k^2+2k\sum_{i=1}^{10}i+\sum_{i=1}^{10}i^2\\ &=10k^2+110k+385 \end{align*} $x_i=S-a_i^2$ тул $$10k^2+110k+385-9(k+10)^2>0\Leftrightarrow k^2-70k-515>0$$ байхаар $k\in\mathbb N$ тоо сонгоход $x_i$ тоонууд натурал тоо байна. $k=77$ үед $$77^2-70\cdot 77-515=24>0$$ тул $$S=10\cdot 77^2+110\cdot 77+385=68145$$ ба $a_i=3(77+i)$ тоонуудын хувьд $x_i=68145-a_i^2$ тоонууд бодлогын нөхцөлийг хангана. Эдгээр нь $$24,1581,3120,4641,6144,7629,9096,10545,11976,13389$$ тоонууд юм.
$a_i=3(k+i)$, $i\in[10]$ байхаар сонговол \begin{align*} S&=\sum\limits_{i=1}^{10} (k+i)^2=\sum_{i=1}^{10}(k^2+2ki+i^2)\\ &=10k^2+2k\sum_{i=1}^{10}i+\sum_{i=1}^{10}i^2\\ &=10k^2+110k+385 \end{align*} $x_i=S-a_i^2$ тул $$10k^2+110k+385-9(k+10)^2>0\Leftrightarrow k^2-70k-515>0$$ байхаар $k\in\mathbb N$ тоо сонгоход $x_i$ тоонууд натурал тоо байна. $k=77$ үед $$77^2-70\cdot 77-515=24>0$$ тул $$S=10\cdot 77^2+110\cdot 77+385=68145$$ ба $a_i=3(77+i)$ тоонуудын хувьд $x_i=68145-a_i^2$ тоонууд бодлогын нөхцөлийг хангана. Эдгээр нь $$24,1581,3120,4641,6144,7629,9096,10545,11976,13389$$ тоонууд юм.
2. $a^2+b^2+c^2=1$ байх эерэг бодит $a,b,c$ тоонуудын хувьд
$$\dfrac{a^2}{a^2+2}+\dfrac{b^2}{b^2+2}+\dfrac{c^2}{c^2+2}<\dfrac12$$
тэнцэтгэл биш биелэхийг батал.
Заавар Бодолт
Заавар. $2 < a^2+2$ ашиглан хуваарийг багасга.
Бодолт. $$\dfrac{a^2}{a^2+2}+\dfrac{b^2}{b^2+2}+\dfrac{c^2}{c^2+2}<\dfrac{a^2}{2}+\dfrac{b^2}{2}+\dfrac{c^2}{2}=\dfrac12$$
3. $1$-ээс их $n$ натурал тоо болон $p$ анхны тооны хувьд $p-1$ нь $n$-д хуваагддаг ба $n^3-1$ нь $p$-д хуваагддаг бол $4p-3$ нь бүтэн квадрат болно гэж харуул.
Заавар Бодолт
Заавар. $n\mid p-1$ тул $n \le p-1$ байна. Иймд $(p,n-1)=1$ тул $p\mid n^3-1=(n-1)(n^2+n+1)\Rightarrow p\mid n^2+n+1$ болно.
Бодолт. $p-1\mid n$ тул $n\mid n^2+n+1-p$ ба $p\mid n^2+n+1$ тул $p\mid n^2+n+1-p$ байна. Түүнчлэн $(n,p)=1$ тул
$$n^2+n+1-p=pnk$$
байна. Хэрвээ $k\neq0$ бол $n^2+n+1\ge pn+p=p(n+1)\ge(n+1)^2$ болж зөрчил үүснэ. Иймд $k=0$ буюу $p=n^2+n+1$
болов. Иймд
$$4p-3=4n^2+4n+1=(2n+1)^2$$
болж батлах зүйл батлагдав.
4. $ABC$ гурвалжны $AB$ талын дундаж цэг нь $D$ ба $AC$ тал дээр $AE=2\cdot EC$ байх $E$ авав. Хэрэв $CD$ ба $BE$ хэрчмүүдийн огтлолын цэгийг $K$ гэвэл $DBK$, $KBC$ гурвалжнуудын талбай тэнцүү болохыг батал.
Заавар Бодолт
Заавар. $D$ ба $C$ цэгүүдийг дайруулж $BE$ хэрчимтэй параллел шулуун тат.
Бодолт.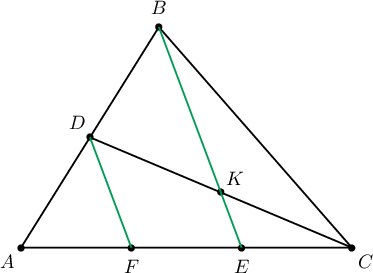 
Зурагт үзүүлснээр $DF\parallel AE$ хэрчим татъя. Тэгвэл Фалесийн теоремоор
$$AF=FE=\dfrac{AE}{2}=EC$$
болно. Эндээс $KE$ нь $\triangle DCF$ гурвалжны дундаж шугам байна. Иймд $DK=KC$ байна. $BK$ нь $DBC$ гурвалжны медиан тул талбайг нь хагаслан хуваана. Иймд $DBK$, $KBC$ гурвалжнуудын талбай тэнцүү болов.