Сайн гараа 2018, 5-р анги
Бодлогын тоо: 4 Хугацаа: мин
1. 1-ээс 9 хүртэлх цифрүүдийг нэг нэг удаа ашиглан бичсэн 11-д хуваагддаг 9 оронтой хамгийн их тоог ол.
Заавар Бодолт
Заавар. Хэрвээ ямар нэг натурал тооны цифрүүдийг нэг нэгээр нь салгаж бичээд сүүлээс нь эхлэн $+$ ба $-$ тэмдэг сөөлжлүүлэн тавиад гарсан илэрхийллийг бодоход гарах тоо 11-д хуваагдах бол уг тоо 11-д хуваагдан. Жишээ $121$ тооны хувьд $+1-2+1=0$ нь 11-д хуваагдах тул $121$ тоо 11-д хуваагдана.
Бодолт. 11-д хуваагдах хамгийн их тоогоо $\overline{98765abcd}$ ба $\overline{abcd}$ нь $1,2,3,4$ цифрүүдийг нэг, нэг удаа ашиглан бичиж болох тоо хэлбэрээр хайя. Ийм тоонууд олдвол эдгээрийн хамгийн их нь бидний хайж байгаа тоо болох нь ойлгомжтой. 11-д хуваагдах тооны шинжээр
$$(9+7+5+b+d)-(8+6+a+c)=7+b+d-a-c=11k$$
байх ёстой. Энэ илэрхийлэл нь хамгийн багадаа $7+1+2-3-4=3$, хамгийн ихдээ $7+3+4-1-2=11$ утга авах боломжтой тул $k=1$ байна. Энэ тохиолдолд $b+d=7$, $a+c=3$ ба хамгийн их байхын тулд $a=2$, $b=4$, $c=1$, $d=3$ байна. Өөрөөр хэлбэл бодлогын нөхцөлийг хангах тоо $987652413$ юм.
2. Хоёр оронтой 2 тооны цифрүүдийн үржвэр нь үржигдэхүүн тус бүрийн цифрүүдийг солиход гарах тоонуудын үржвэртэй тэнцүү байв. Жишээ нь $46\cdot 96=64\cdot 69$. Ийм чанартай 2 оронтой бүх хос тоонуудыг ол.
Тайлбар: $\overline{AB}\cdot\overline{BA}$, $\overline{AA}\cdot\overline{BB}$, $\overline{AA}\cdot\overline{AA}$ хэлбэрийн тоонуудыг тооцохгүй.
Тайлбар: $\overline{AB}\cdot\overline{BA}$, $\overline{AA}\cdot\overline{BB}$, $\overline{AA}\cdot\overline{AA}$ хэлбэрийн тоонуудыг тооцохгүй.
Заавар Бодолт
Заавар. Хоёр оронтой тоонуудаа $\overline{ab}$, $\overline{cd}$ гэвэл
$$(10a+b)(10c+d)=(10b+a)(10d+c)$$
байна.
Бодолт. $$(10a+b)(10c+d)=(10b+a)(10d+c)$$
илэрхийллийг гишүүнчлэн үржүүлж задлавал
$$100ac+10(ad+bc)+bd=100bd+10(bc+ad)+ac\Leftrightarrow 99ac-99bd=0$$
тул $ac=bd$ байна. $a$, $b$, $c$, $d$ нь цифрүүд тул дор хая 2 аргаар цифрүүдийн үржвэрт задардаг тоонуудыг олъё. Эдгээр нь
\begin{align*}
1\cdot 4&=2\cdot 2=4 & 12\cdot 42&=21\cdot 24\\
1\cdot 6&=2\cdot 3=3\cdot 2=6 & 12\cdot 63&=21\cdot 36 & 13\cdot 63=31\cdot 36\\
1\cdot 8&=2\cdot 4=4\cdot 2=8 & 12\cdot 84&=21\cdot 48 & 14\cdot82=41\cdot28\\
1\cdot 9&=3\cdot 3=9 & 13\cdot 93&=31\cdot 39\\
2\cdot 6&=3\cdot 4=4\cdot 3=12 & 23\cdot 64&=32\cdot 46 & 24\cdot63=42\cdot36\\
2\cdot 8&=4\cdot 4=16 & 24\cdot 84&=42\cdot 48\\
2\cdot 9&=3\cdot 6=6\cdot 3=18 & 23\cdot 96&=32\cdot 69 & 26\cdot93=62\cdot 96\\
3\cdot 8&=4\cdot 6=6\cdot 4=24 & 34\cdot 86&=43\cdot 68 & 36\cdot 84=63\cdot 48\\
4\cdot 9&=6\cdot 6=36 & 46\cdot 96&=64\cdot 69
\end{align*}
байна.
3. Самбарт $123456789$ гэсэн тоо бичигдсэн байв. Зэрэгцээ бичигдсэн хоёр цифр хоёулаа тэгээс ялгаатай бол тус бүрээс нь 1-ийг хасаад гарсан хоёр цифрүүдийн байрыг сольж бичнэ. Жишээ нь $123{\color{red}{45}}6789$ тооноос үйлдэл хийгээд $123{\color{red}{43}}6789$ тоог гарган авна. Энэ үйлдлийг давтах замаар хамгийн багадаа ямар тоог гарган авч чадах вэ?
Заавар Бодолт
Заавар. Энэ үйлдлээр цифрүүдийн тэгш сондгой хадгалагдаж үлдэхийг харуул.
Бодолт. Дараалсан хоёр цифр нь $CT$ байсан 1, 1-ийг хасахад $T, C$ болох ба байрыг нь солиход буцаад $CT$ болно. $TC$ үед мөн адил $TC$ болох нь ойлгомжтой юм. Анх цифрүүд тэгш сонгойгоороо сөөлжилж байрласан байсан тул энэ байрдал буюу $CTCTCTCTC$ хэлбэрээ хадгална. Ийм хамгийн бага тоо нь мэдээж $101010101$ юм. Энэ тоог гаргаж авч чадахыг харуулахад төвөгтэй биш юм. Үнэндээ
$$89\to 87\to 67\to 65\to 45\to 43\to 23\to 21\to 01$$
үйлдлийг ашиглаад $23$, $45$, $67$, $89$ тоонуудыг $01$ болгож болох тул $101010101$ тоог ч мөн адил гарган авах боломжтой юм.
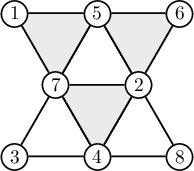
4. 1-ээс 8 хүртэлх тоонуудыг будагдсан гурвалжны орой дахь 3 тооны нийлбэр 13 байхаар, будагдаагүй гурвалжны орой дахь 3 тооны нийлбэр 14 байхаар байршуул.